Без учета депланации в стальных стержнях получаем завышенные перемещения

Расчёт стальных стержней на действие нагрузки, вызывающей поперечную силу и крутящий момент, следует применять шестой признак схемы и седьмой тип КЭ, который позволяет учесть секториальный момент инерции. Без учёта седьмой степени свободы в результатах расчёта, будут завышенные значения деформаций кручения в стержне.

Пример учёта секториального момента инерции

Рассмотрим пример: задана балка длиной 6 м, с жёстким защемлением по краям. Поперечное сечение балки — двутавр 35Б2. К балке, в уровне верхнего пояса, приложена поперечная сила, интенсивностью 1 т. Расстояние между центром жёсткости балки и точкой приложения силы (плечо), составляет 0.2 м.

Расчётная модель балки

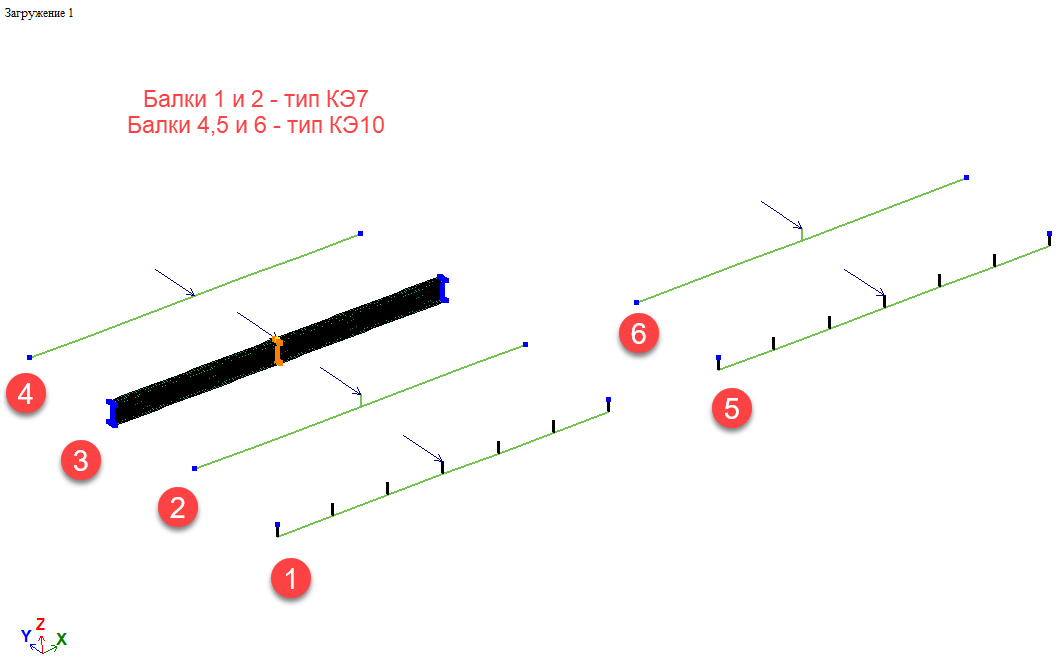
Для эксперимента, подготовим несколько вариантов расчётной модели балки:

1. Балка моделируется стержнем. Сила приложена в уровне оси балки. Плечо силы, моделируется заданием жёсткой вставки. Тип КЭ7;
2. Балка моделируется стержнем. Сила приложена на расстоянии 0.2 м от оси балки. Передача крутящего момента от силы, обеспечивается стержнем большой жёсткости, который соединяет точку приложения силы и ось балки. Тип КЭ7;
3. Объёмная модель балки из пластинчатых КЭ. Сила прикладывается в уровне верхнего пояса. Узлы, находящиеся в одной плоскости с вектором действия поперечной силы, объединены в АЖТ;
4. Балка моделируется стержнем. Сила приложена в уровне оси балки. Плечо не моделируется, с целью определить горизонтальный прогиб балки без крутящего момента. Тип КЭ10;
5. Модель аналогична балке №1. Тип КЭ10;
6. Модель аналогична балке №2. Тип КЭ10;

Для данной задачи выбран 6-й признак схемы:

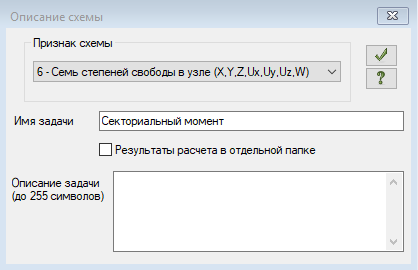
Признак схемы №6 обеспечивает 7 степеней свободы в узле, что позволяет учесть секториальный момент.

Обязательным условием учёта в работе схемы секториального момента, является назначение элементам схемы КЭ тип 7, в противном случае, секториальный момент учитываться не будет.

Балка №3, смоделированная пластинами, служит в качестве модели, максимально приближенной к работе реальной конструкции. Её деформации, в рамках данной задачи, будут считаться эталонными.

Результаты расчёта

После выполнения статического расчёта, выполним сравнение перемещений узлов, к которым приложена нагрузка. Сравниваем перемещения вдоль оси Y:

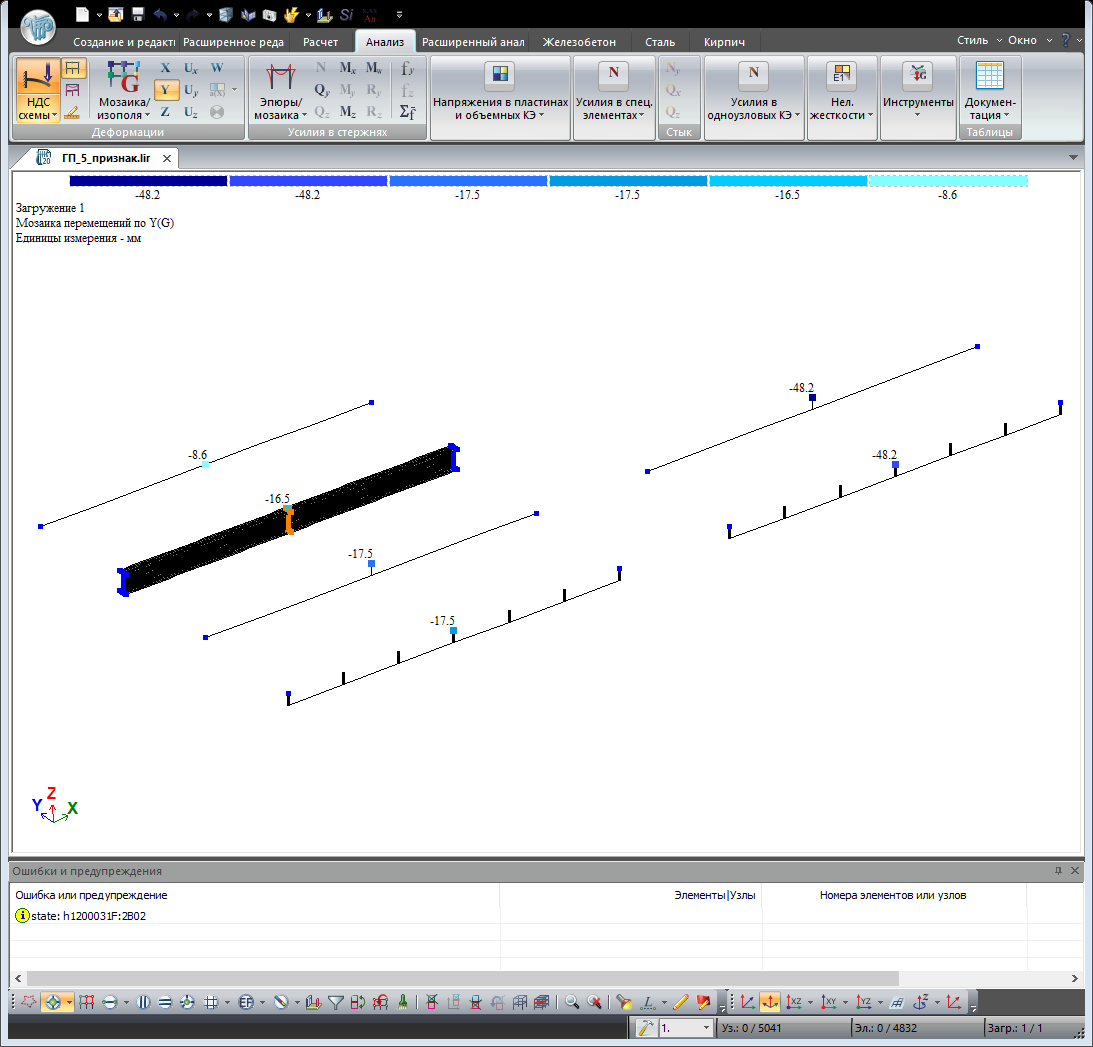
Сравнение результатов расчёта:

Балка №1 – 17.5 мм;
Балка №2 — 17.5 мм;
Балка №3 — 16.5 мм – эталонный результат;
Балка №4 — 8.5 мм – горизонтальный прогиб балки в уровне её оси;
Балка №5 — 48.2 мм;
Балка №6 — 48.2 мм;

Как видно, наибольшая сходимость результатов с эталоном, наблюдается у моделей 1 и 2, где учтён секториальный момент. В моделях 5 и 6, где секториальный момент не учитывается, результат завышен.

Разберёмся, из чего складывается перемещение узла, на который действует нагрузка.

Определение перемещения узла, при действии поперечной силы и крутящего момента

При действии поперечной силы и крутящего момента, балка будет испытывать горизонтальный прогиб, который вызовет горизонтальное перемещение в уровне её оси, равное 8.5 мм – результат балки №4. Крутящий момент, вызовет поворот поперечного сечения вокруг продольной оси балки, из-за чего, узел, на который действует нагрузка, дополнительно переместится на величину равную L*UX, где L – плечо силы (расстояние от точки приложения силы до оси балки), UX – угол поворота поперечного сечения вокруг оси балки.

Итоговое перемещение точки приложения силы считается по формуле Δ=Δy+L*UX. Исходные данные для вычислений, берём из результатов расчёта:

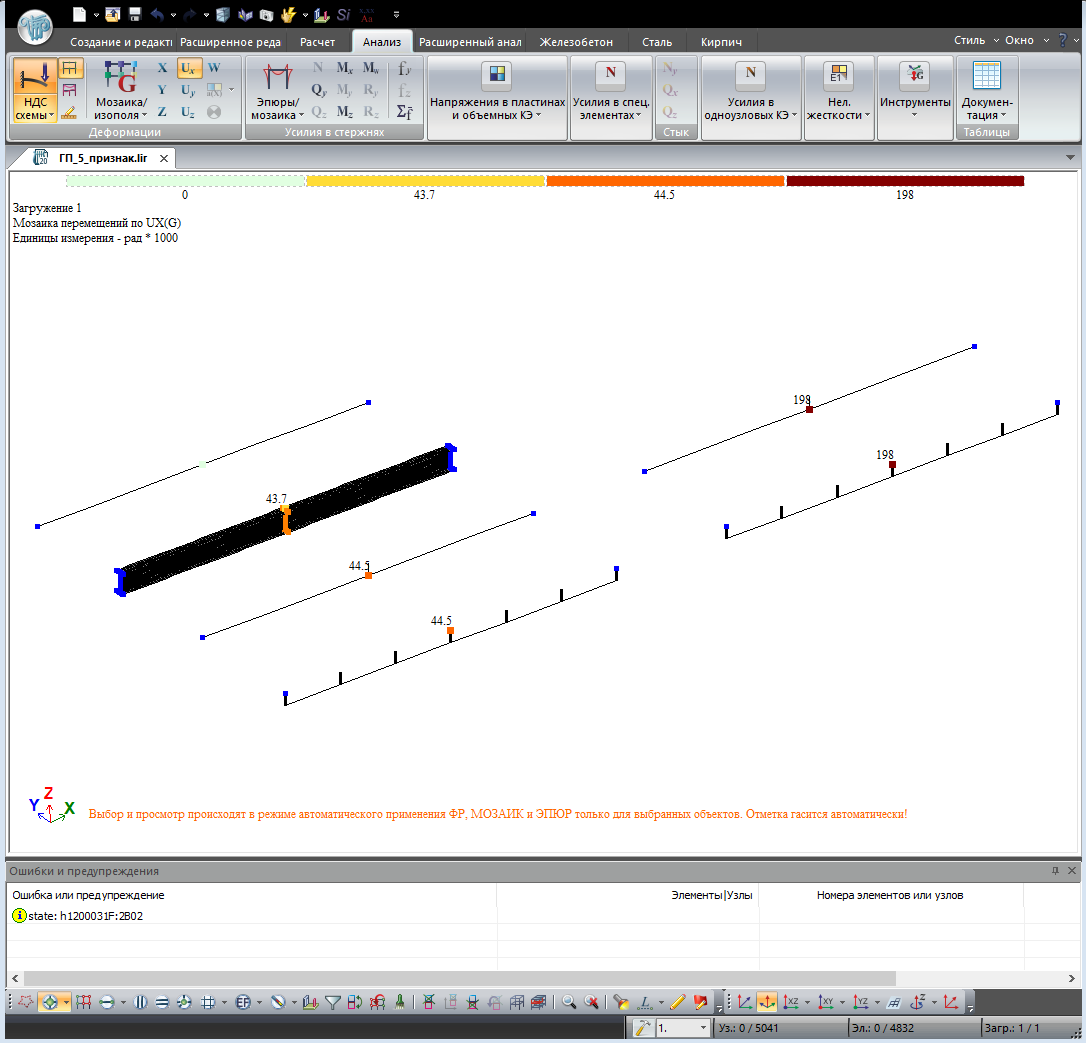
Определим перемещение точки приложения силы вдоль оси Y:

Балки №1 и №2 Δ=Δy+L*UX=8.5 мм + 200 мм * 44.5/1000 рад = 17.4 мм
Балки №5 и №6 Δ=Δy+L*UX=8.5 мм + 200 мм * 198/1000 рад = 48.1 мм

Из поставленного эксперимента, можно сделать вывод, что при расчёте стальных стержней подобного сечения (двутавр, швеллер, С-образный и т.п.) на действие крутящего момента, следует применять 6-й признак схемы и тип КЭ7, чтобы получить работу модели, максимально приближенную к действительной работе конструкции.

Кроме того, в СП 16.13330.2017 есть несколько проверок, которые требуют учета бимомента. А для этого нужно его еще получить.

8.2 Расчет на прочность изгибаемых элементов сплошного сечения.

8.2.1 Расчёт на прочность балок 1-го класса при действии моментов в двух главных плоскостях (и наличии бимомента) следует выполнять по формуле 43:

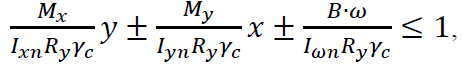
8.4 Расчет на общую устойчивость изгибаемых элементов сплошного сечения.

8.4.1 Расчёт на устойчивость двутавровых балок 1-го класса, а также бистальных балок 2-го класса, удовлетворяющих требованиям 8.2.1 и 8.2.8, при изгибе в двух главных плоскостях (и наличии бимоментов) следует выполнять по формуле 70:

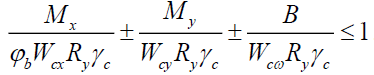
9.1 Расчёт на прочность элементов сплошного сечения.

9.1.1 Расчёт на прочность внецентренно сжатых (сжато-изгибаемых) и внецентренно растянутых (растянуто-изгибаемых) элементов из стали с нормативным сопротивлением Ryn≤440 Н/мм², не подвергающихся непосредственному воздействию динамических нагрузок, при напряжениях τ<0,5Rs и σ=N/An> 0,1Ry следует выполнять по формуле 105:

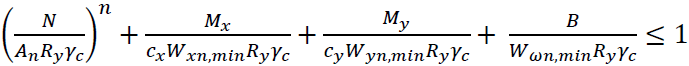
Расчёт на прочность элементов в случаях, не предусмотренных расчётом по формуле (105), следует выполнять по формуле 106:

где:

х и у — расстояния от главных осей до рассматриваемой точки сечения, а ω – секториальная координата этой точки;
B — бимомент, изгибно-крутящий бимомент;
Wсω — секториальный момент сопротивления сечения, вычисленный для наиболее сжатой точки сжатого пояса;
Iwn — секториальный момент инерции сечения нетто.