Расчет прогибов ЖБК в соответствии нормами СП 63.13330.ХХХХ
Ниже описываются требования норм к расчету прогибов железобетонных элементов и их реализация в ПК ЛИРА-САПР.
Расчет прогибов в соответствии с СП 63.13330.ХХХХ определяется на основании кривизны железобетонного элемента.
8.2.24 Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяют по формулам:
- для участков без трещин в растянутой зоне:
1/r=(1/r)1+(1/r)2 (8.140)
- для участков с трещинами в растянутой зоне:
1/r=(1/r)1-(1/r)2+(1/r)3 (8.141)
В формуле (8.140):
(1/r)1, (1/r)2 – кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и временных длительных нагрузок.
В формуле (8.141):
(1/r)1 – кривизна от непродолжительного действия всей нагрузки, на которую производят расчет по деформациям;
(1/r)2 – кривизна от непродолжительного действия постоянных и временных длительных нагрузок;
(1/r)3 – кривизна от продолжительного действия постоянных и временных длительных нагрузок.
Кривизна железобетонного элемента определяется в зависимости от его изгибной жесткости D, которая зависит от модуля деформаций бетона Eb1 и приведенного момента инерции сечения Ired.
Изгибная жесткость D элемента определяется с учетом того, образовались или нет на данном участке нормальные трещины.
8.2.25 Кривизну железобетонных элементов 1/r от действия соответствующих нагрузок (см. 8.2.24) определяют по формуле
1/r=M/D, (8.142)
где М – изгибающий момент от внешней нагрузки (с учетом момента от продольной силы N) относительно оси, нормальной плоскости действия изгибающего момента и проходящей через центр тяжести приведенного поперечного сечения элемента;
D – изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле
D=Eb1*Ired, (8.143)
где Eb1 – модуль деформации сжатого бетона, определяемый в зависимости от продолжительности действия нагрузки и с учетом наличия или отсутствия трещин;
Ired – момент инерции приведенного поперечного сечения относительно его центра тяжести, определяемый с учетом наличия или отсутствия трещин.
Значения модуля деформации бетона Еb1 и момента инерции приведенного сечения Ired для элементов без трещин в растянутой зоне и с трещинами определяют по 8.2.26 и 8.2.27 соответственно.
Значения модуля деформации бетона в формулах (8.143), (8.145) принимают равными:
– при непродолжительном действии нагрузки
Eb1=0.85Eb, (8.146)
– при продолжительном действии нагрузки
Eb1=Ebτ=Eb1/(1+φb,cr) (8.147)
где φb,cr принимают по таблице 6.12.
ПК ЛИРА-САПР при определении прогибов элементов оперирует их жесткостью. При таком подходе полученные прогибы следует суммировать аналогично кривизне
8.2.31 Прогибы железобетонных элементов можно определять по общим правилам строительной механики с использованием вместо кривизны 1/r непосредственно изгибных жесткостных характеристик D путем замены упругих изгибных характеристик EI в расчетных зависимостях на характеристики D, вычисляемые по формулам, приведенным в 8.2.25 и 8.2.29.
При совместном действии кратковременной и длительной нагрузок полный прогиб элементов без трещин и с трещинами в растянутой зоне определяют путем суммирования прогибов от соответствующих нагрузок по аналогии с суммированием кривизны по 8.2.24, принимая жесткостные характеристики D в зависимости от указанной в этом пункте принятой продолжительности действия рассматриваемой нагрузки.
Допускается при определении жесткостных характеристик D элементов с трещинами в растянутой зоне принимать коэффициент ψs= 1. В этом случае при совместном действии кратковременной и длительной нагрузок полный прогиб изгибаемых элементов с трещинами определяют путем суммирования прогибов от непродолжительного действия кратковременной нагрузки и от продолжительного действия длительной нагрузки с учетом соответствующих значений жесткостных характеристик D, т. е. подобно тому, как это принято для элементов без трещин.
Пример.
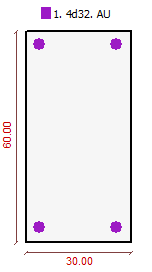
Прямоугольный свободно опертый элемент пролетом 4800мм. Бетон класса В15, арматура – А500. Размеры сечения: b=300мм h=600мм, a=a’=40мм. Продольная арматура 4d32. На элемент действует равномерно распределенная нагрузка – длительная 75кН/м и кратковременная 15кН/м. Кроме того приложена продольная растягивающая сила – длительная 16кН и кратковременная 10кН. Влажность воздуха лежит в диапазоне 40-75%.
Расчет ведем в физически нелинейной постановке.
Для описания диаграммы σ-ε применяем 14й закон деформирования – трехлинейную диаграмму деформирования для бетона и двухлинейную для арматурной стали. Т.к. работа материала описывается диаграммой σ-ε, а не модулем деформаций, то влияние кратковременной и длительной ползучести реализовывается путем умножение значений относительных деформаций бетона εb1 и εbt1 на коэффициенты 1/0.85=1.176 и 1+φb,cr=1+3.4=4.4 соответственно. Такой подход аналогичен, по своей сути, формулам (8.146) и (8.147).
Относительные деформации εb0 ,εb2, εbt0, εbt2 принимаются в зависимости от длительности действия нагрузок: εb0=-0.002, εb2=-0.0035, εbt0=0.0001, εbt2=0.00015 при кратковременном действии нагрузок, εb0=-0.0034, εb2=-0.0048, εbt0=0.00024, εbt2=0.00031 при длительном действии нагрузок (таблица 6.10 СП 63).
На участках с трещинами принимается диаграмма работы бетона без учета растянутой ветви.
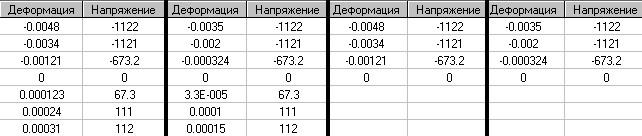
Исходная диаграмма σ-ε бетона класса В15
| ε | σ,тс/м2 |
| -0.003500 | -1122.00 |
| -0.002000 | -1121.00 |
| -0.000275 | -673.20 |
| 0.000000 | 0.00 |
| 0.000028 | 67.32 |
| 0.000100 | 111.00 |
| 0.000150 | 112.20 |
Диаграмма σ-ε бетона класса В15 с учетом кратковременной ползучести
| ε | σ,тс/м2 |
| -0.003500 | -1122.00 |
| -0.002000 | -1121.00 |
| -0.000324 | -673.20 |
| 0.000000 | 0.00 |
| 0.000033 | 67.32 |
| 0.000100 | 111.00 |
| 0.000150 | 112.20 |
Диаграмма σ-ε бетона класса В15 с учетом длительной ползучести
| ε | σ,тс/м2 |
| -0.0048 | -1122.00 |
| -0.0034 | -1121.00 |
| -0.001210 | -673.20 |
| 0.000000 | 0.00 |
| 0.000123 | 67.32 |
| 0.00024 | 111.00 |
| 0.00031 | 112.20 |
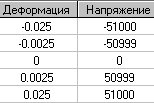
Диаграмма σ-ε арматуры класса А500
| ε | σ,тс/м2 |
| -0.025 | -51000 |
| -0.0025 | -50999 |
| 0 | 0 |
| 0.0025 | 50999 |
| 0.025 | 51000 |
Момент инерции сечения Ired определяется автоматически в зависимости от полученного во время расчета НДС нормального сечения.
Таким образом, во время физически нелинейного расчета ПК ЛИРА-САПР определяет жесткостные характеристики элементов автоматически.
По длине балки назначается 2 типа жесткости – с учетом работы растянутой ветви (для участков без трещин) и без этого учета (на участках с трещинами).
Типы жесткости:
1 – диаграмма σ-ε с учетом длительной ползучести и учетом растянутой ветви работы бетона;
2 – диаграмма σ-ε с учетом кратковременной ползучести и учетом растянутой ветви работы бетона;
3 – диаграмма σ-ε с учетом длительной ползучести, без учета растянутой ветви работы бетона;
4 – диаграмма σ-ε с учетом кратковременной ползучести, без учета растянутой ветви работы бетона.
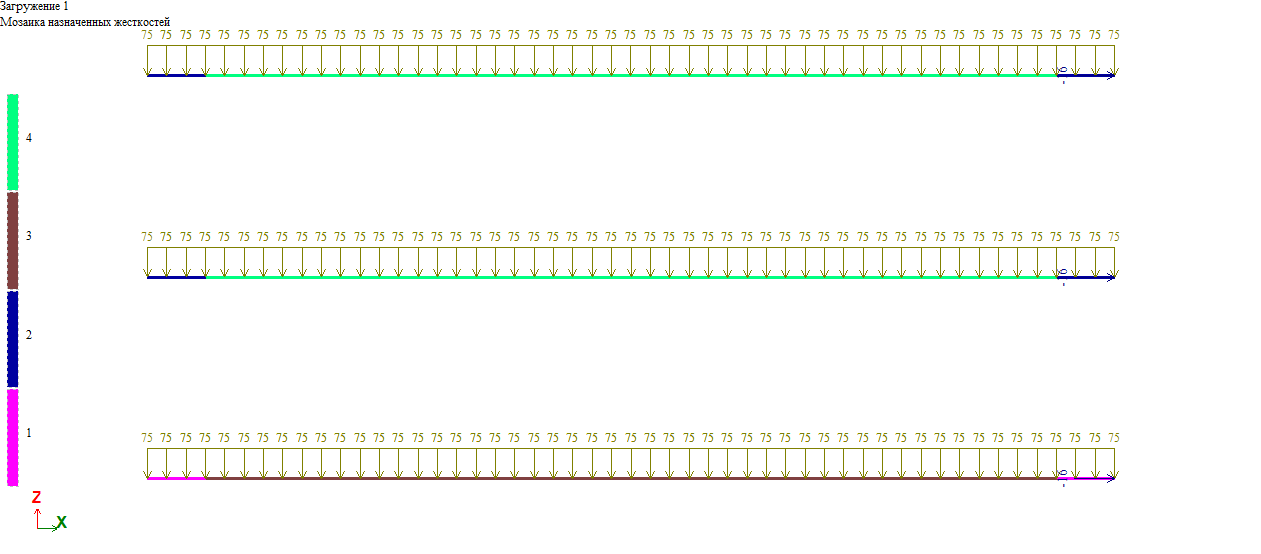
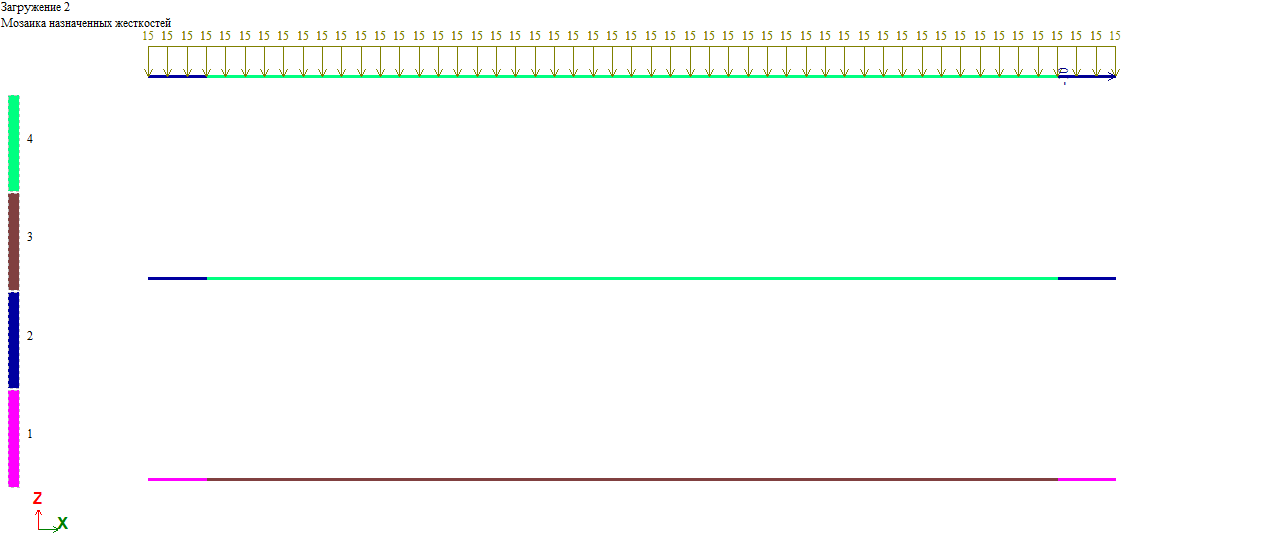
Нагрузки прикладываем в 2х загружениях: загружение 1 – длительные нагрузки, загружение 2 – кратковременные.
Для получения трех составляющих прогибов f1, f2, f3 создаем 3 балки:
балка 1 – характеристики жесткости, соответствующие кратковременной ползучести; нагрузка 75кН/м в загружении 1 и 15кН/м в загружении 2;
балка 2 – характеристики жесткости, соответствующие кратковременной ползучести; нагрузка 75кН/м в загружении 1;
балка 3 – характеристики жесткости, соответствующие длительной ползучести; нагрузка 75кН/м в загружении 1.
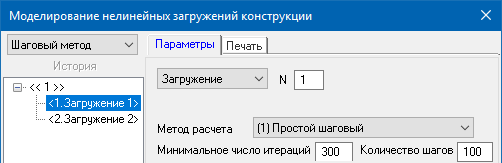
Для выполнения нелинейного расчета следует задать шаговую историю нагружения:
Результаты расчета:
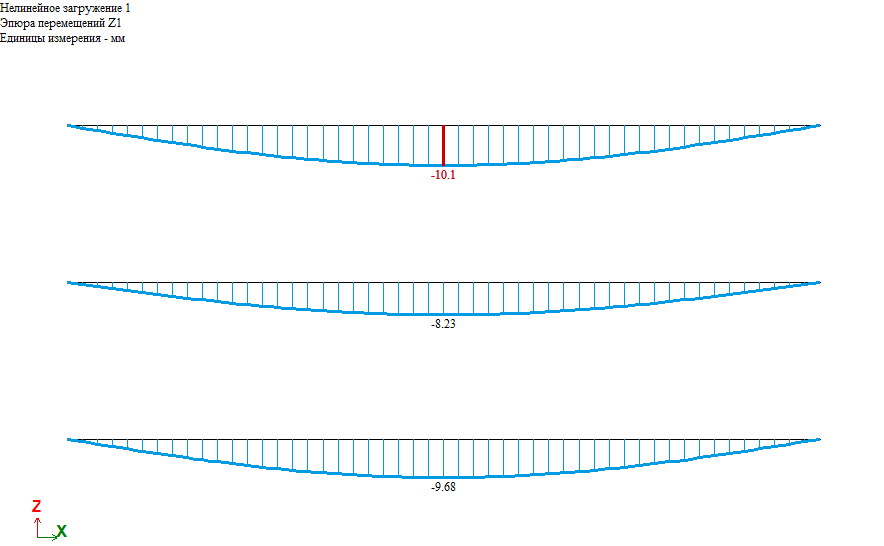
Прогиб балки составляет:
f=f1-f2+f3=10.1-8.23+9.68=11.55мм
