Гармоническая нагрузка, пример расчета балки
Ниже приведен пример ручного и компьютерного расчета свободно опертой балки на гармонические колебания.
Исходные данные:
пролет балки l=6м; размеры поперечного сечения bxh=0.3x0.5м;
бетон класса В25 (Eb=30000МПа=3060000тс/м2);
в середине пролета установлен электродвигатель весом Gд=2тс;
вес возвратно-поступательно вращающейся части двигателя (ротора) G=0.25тс;
амплитуда перемещения центра масс (радиус эксцентрика) е=0.01м;
частота вращения n=600об/мин; коэффициент неупругого сопротивления колебаниям γ=0.1
Ручной расчет
Определим расчетное амплитудное значение динамической нагрузки согласно [1] стр. 13-14:
R = kдmeθ2 = 1.3 * 0.0255 * 0.01 * 63.832 = 1.35 тс,
где kд = 1.3 — коэффициент перегрузки для машин с конструктивно-неуравновешенными движущимися частями;
m=G/g=0.25/9.807=0.0225т — масса ротора;
θ=πn/30=3.14*600/30=63.83рад/с — круговая частота вращения ротора.
Расчетный момент от статической нагрузки:
Mc = γf,св * qсв *l2/8 + γf,об * G * l/4 = 1.1 * 0.375 * 62/8 + 1.05 * 2 * 6/4 = 5тс * м,
где qсв = b * h * ρ = 0.3 * 0.5 * 2.5 = 0.375 тс/м — нормативное значение погонной нагрузки от собственного веса балки;
ρ = 2.5 тс/м3 — объемный вес железобетона;
γf = 1.1 — коэффициент надежности по нагрузке для собственного веса;
γf,об = 1.05 — коэффициент надежности по нагрузке для веса двигателя.
Расчетный момент от динамической нагрузки может быть определен путем статического ее приложения с учетом коэффициента динамичности:
Mд = μ * R * l/4 = 2.354 * 1.35 * 6/4 = 4.77тс * м,
где μ – коэффициент динамичности [2] стр. 48:
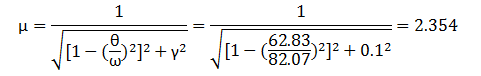
где ω=82.07рад/с – круговая частота собственных колебаний по 1й (основной) форме (определение см. ниже).
Расчетное значение изгибающего момента для расчета на прочность:
M = Mc + Mд = 5 + 4.77 = 9.77 тс * м.
Расчет в ПК ЛИРА САПР
Модуль 24
Балка (размеры поперечного сечения bxh=300х500мм из бетона В25) загружается 3-мя нагрузками. Значения всех нагрузок расчетные.
Собственный вес:
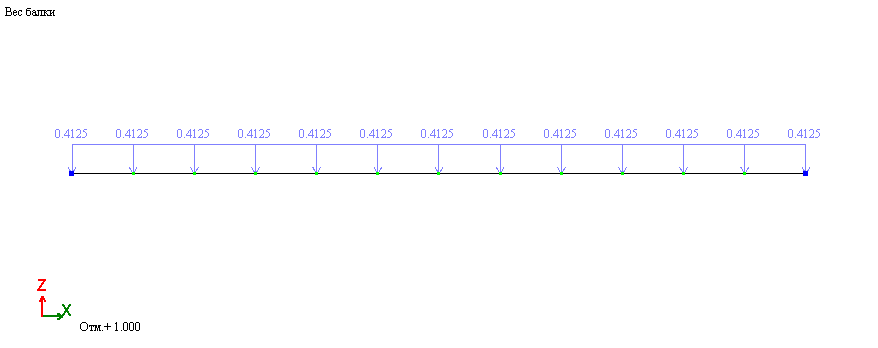
Вес двигателя:
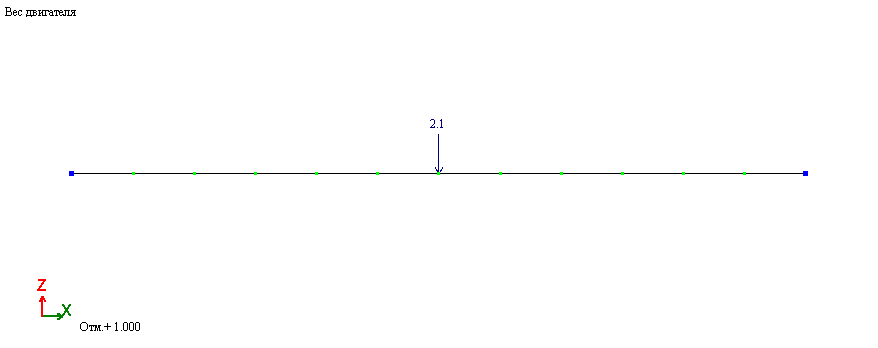
Гармоническая нагрузка:

После приложения нагрузок задаем характеристики расчета на динамические воздействия:
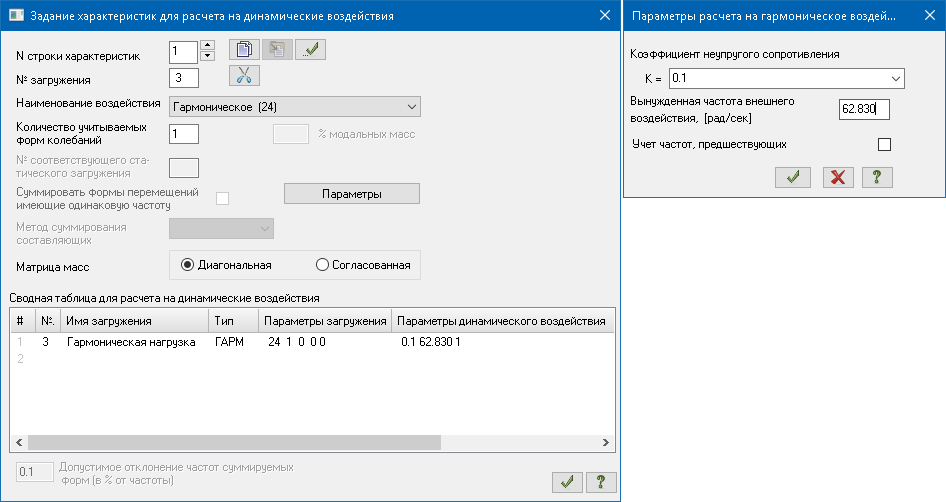
Собираем веса масс из загружений 1 и 2:
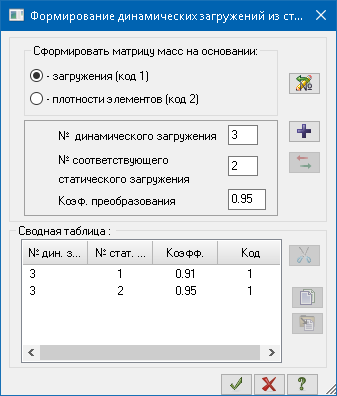
Коэффициенты преобразования приняты равными коэффициентам, обратным коэффициентам надежности по нагрузке: 1/1.1=0.91 и 1/1.05=0.95. Формируем таблицу РСУ:
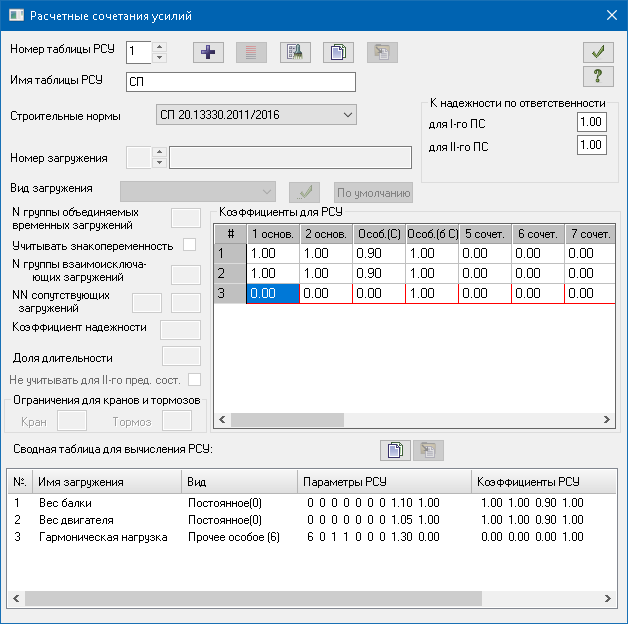
Результаты расчета:
Таблица частотных характеристик:

Огибающая эпюра изгибающих моментов (РСУ)
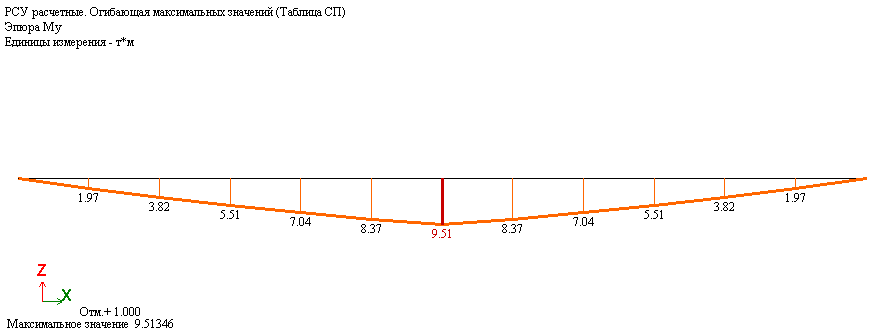
Модуль Динамика +
Модуль Динамика + предполагает определенную последовательность загружений: первыми в расчетной модели должны быть приложены статические нагрузки, а затем загружения с весами масс, динамической нагрузкой и, при необходимости, демпфирующими узловыми нагрузками.
Для приложения нескольких статических нагрузок следует сформировать историю нагружения. Для упругих расчетных моделей это реализовывается путем заполнения монтажной таблицы. Возможен и другой вариант – приложение всех статических нагрузок в первом загружении.
Список загружений при расчете балки с использованием модуля Динамика +:
1. Статические нагрузки (собственный вес + вес двигателя):
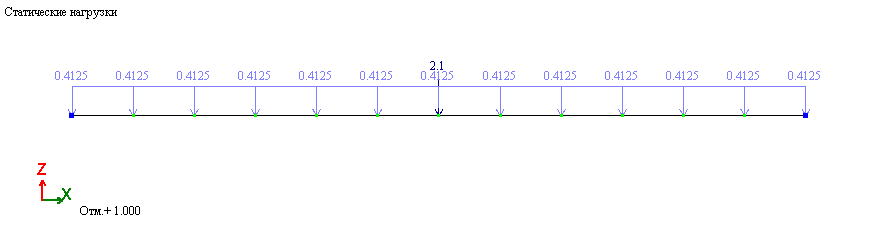
2. Веса масс:
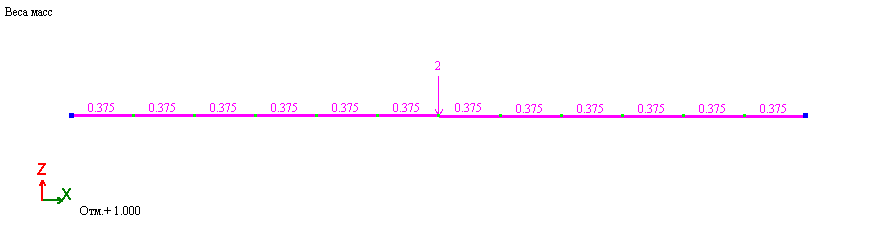
Нагрузки от веса массы приложены вручную. Возможен сбор весов масс аналогичный модулю 24. Для этого следует создать фиктивное загружение, с соответствующими величинами статических нагрузок (в данном случае нормативной величины). Из этого статического собираются веса масс с коэффициентом преобразования 1.
3. Динамика + (тип нагрузки 2 — синусоидальная):
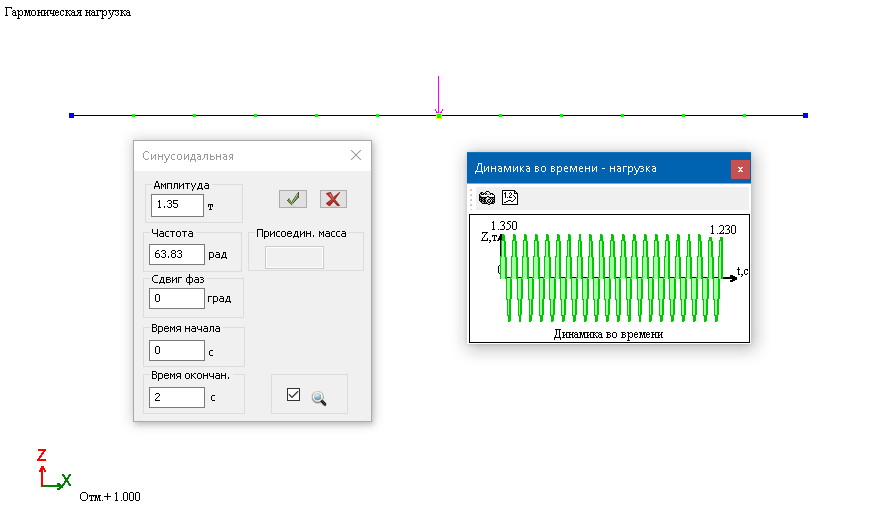
Время окончания нагрузки принято произвольным. По результатам расчета время может быть подкорректировано из условия достижения балкой уравновешенных колебаний.
Демпфирование в ПК ЛИРА-САПР на выбор пользователя может быть смоделировано 2мя способами: либо путем задания узловых нагрузок, либо путем назначения элементам схемы коэффициентов Рэлея (https://help.liraland.ru/984/3158/).
Узловые нагрузки, характеризующие демпфирующие свойства конструкции, могут быть определены по формуле [3] стр. 48:
Ci = 2ξ * mi * ω,
где ξ — параметр затухания в долях от критического (коэффициент диссипации), который может быть определен через логарифмический декремент затухания колебаний δ: ξ=δ/2π или через величину коэффициента неупругого сопротивления γ: ξ=γ/2;
mi — масса в i-м узле;
ω — круговая частота колебаний.
В привязке к рассматриваемой задаче:
- параметр затухания (коэффициент диссипации) ξ=γ/2=0.1/2=0.05;
- вес массы в промежуточном узле Qпр=0.375*0.5=0.1875тс, где 0.5м – шаг узлов;
- вес массы в центральном узле Qц=Qпр+Qдв=0.1875+2=2.1875тс.
- круговая частота колебаний ω=82.07рад/с.
Таким образом, нагрузка демпфер:
Спр = 2 * 0.05 * (0.1875/9.81) * 82.07 = 0.157 тс*с/м;
Сц = 2 * 0.05 * (2.1875/9.81) * 82.07 = 1.830 тс*с/м.
Нагрузки прикладываются как узловые:
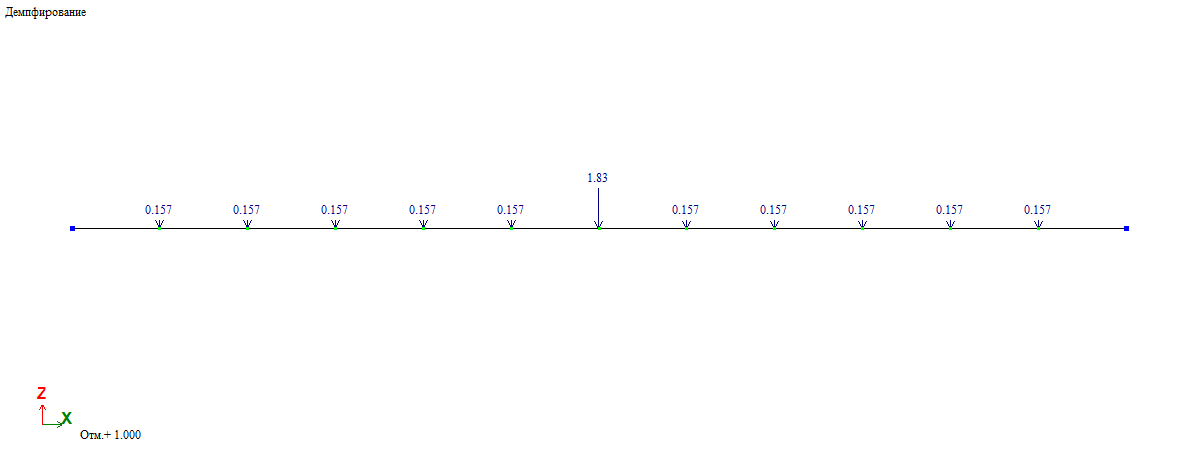
При описании матрицы демпфирования по Рэлею соответствующие коэффициенты могут быть получены исходя из решения системы уравнений:
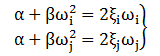
где ωi,j — круговые частоты i и j форм колебаний (i ξi,j — коэффициенты диссипации i и j форм колебаний.
Таким образом, коэффициенты Рэлея можно определить по формулам:
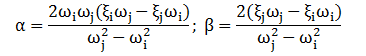
При рассмотрении только одной формы колебаний один из коэффициентов Рэлея можно принять равным нулю. При β=0 имеем: α=2ξω=2*0.05*82.07=8.207.
Коэффициенты Рэлея назначаются элементам схемы как свойство:
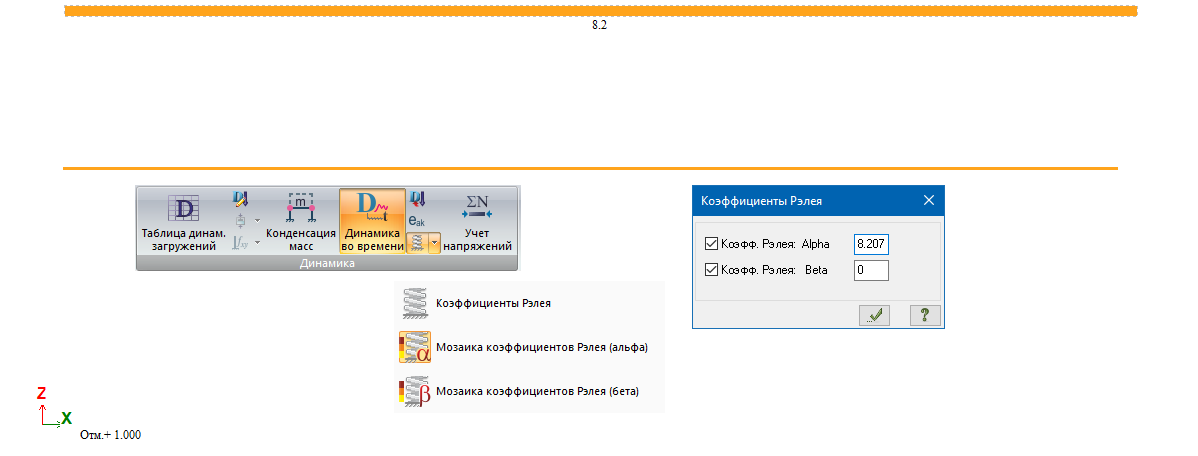
Задаем данные для расчета в процессоре Динамика +:
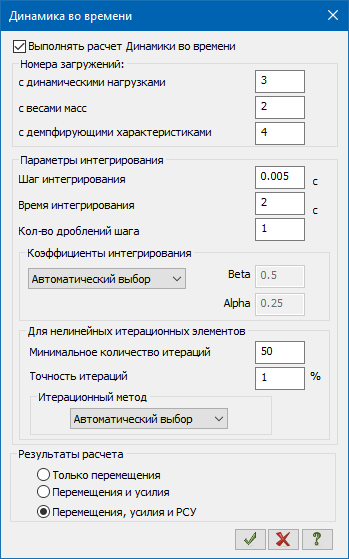
Шаг интегрирования не более 1/10-1/15 от периода колебаний Δt=Т/15=0.0765/15=0.0051с. Принимаем Δt=Т/15=0.0765/15=0.005с. Время интегрирования принимаем равным времени воздействия.
Результаты расчета
Эпюра изгибающих моментов в момент времени 1.21с (установившиеся колебания):
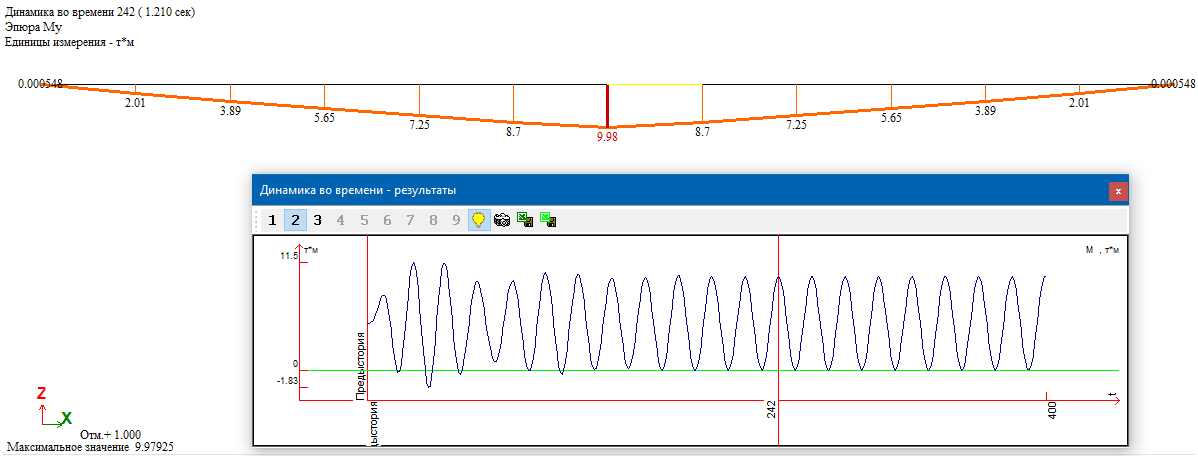
Сравнение результатов расчета
| Сравниваемый параметр | Ручной расчет | Расчет в ПК ЛИРА САПР (модуль 24) | Расчет в ПК ЛИРА САПР (Динамика +) |
| Максимальный изгибающий момент Mmax, тс*м | 9.77 | 9.51 | 9.89 |
Используемая литература
- Инструкция по расчету несущих конструкций промышленных зданий и сооружений на динамические нагрузки. — М.: Стройиздат, 1970.
- А. Ф. Смирнов, А. В. Александров, Б. Я. Лащеников, Н. Н. Шапошников «Строительная механика. Динамика и устойчивость сооружений». — М.: Стройиздат, 1984.
- Р. Клаф, Пензиен Дж. Динамика сооружений — М.: Стройиздат, 1979
