Диаграммы для физической нелинейности
Реализация физически нелинейного расчета
Физически нелинейный расчет выполняется с использованием шагового процессора который позволяет получить напряженно-деформированное состояние с учетом нелинейных эффектов как для мономатериальных, так и для биматериальных конструкций.
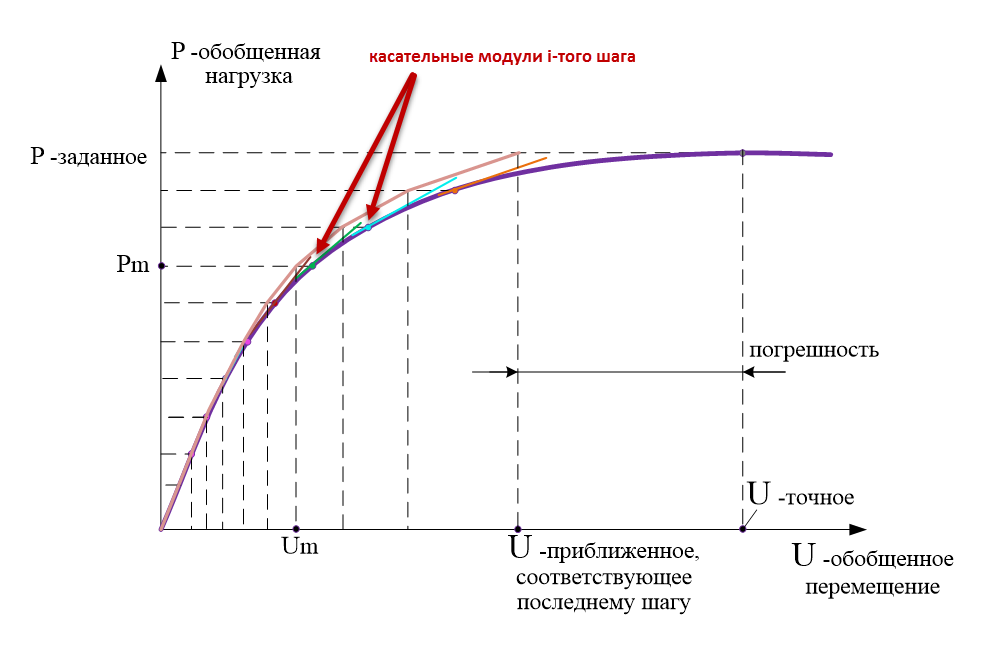
Матрица жесткости линеаризованной физически нелинейной системы формируется на основании переменных интегральных жесткостей, вычисляемых в точках интегрирования конечного элемента при решении упругой задачи на конкретном шаге. Схема численного интегрирования по области конечного элемента и набор используемых жесткостей определяются типом конечного элемента. Для того чтобы получить соответствующий набор интегральных жесткостей, сечение конечного элемента в точках интегрирования дробится на ряд элементарных подобластей. В центрах этих подобластей определяются новые значения физико-механических характеристик материала в соответствии с заданной диаграммой деформирования. На каждом шаге решается линеаризованная задача с формированием векторов перемещений, усилий и новых интегральных жесткостей по касательному модулю для последующего шага. Количество шагов и коэффициенты к нагрузке задаются пользователем. Геометрическая интерпретация шагового метода для случая одноосного растяжения (сжатия) представлена на рисунке ниже
Подробно о методике расчета можно узнать в книге

И почитать статью в Базе знаний от разработчика: https://help.liraland.ru/984/3426/
Описание диаграмм деформирования
При выполнении физ. нелинейного расчета необходимо задать диаграммы деформирования (работы) материалов.
Диаграммы деформирования бетона могут быть приняты из существующей библиотеки (21, 25, 31, 35 законы деформирования) или заданы вручную (14, 15 законы). Для арматуры – 11 и 14 (задаются вручную).
Данные для построения диаграмм, создаваемых пользователем, можно принять из существующих норм на проектирование ж/б конструкций. В этом случае диаграмма описывается 14 кусочно-линейным законом
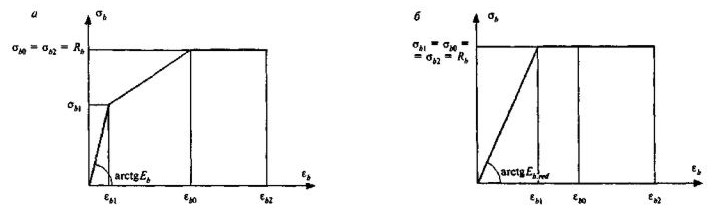
а - трехлинейная диаграмма состояния сжатого бетона; б - двухлинейная диаграмма
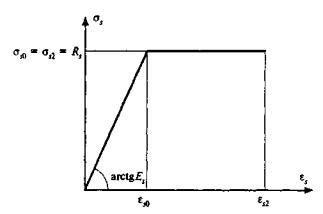
При описании диаграммы 14 законом нельзя моделировать горизонтальные и ниспадающие участки. Таким образом, при построении диаграммы в соответствии с СП 52-2003/СП 63, горизонтальный участок следует моделировать небольшим уклоном площадки пластических деформаций. Следует отметить, что нормативные диаграммы деформирования не учитывают ниспадающую ветвь деформирования бетона (стадию разупрочнения).
Рекомендуем расчет выполнять с использованием стандартных диаграмм работы бетона –25 и 35 законы (в зависимости от того какие нужны характеристики). Для задания произвольных характеристик бетона можно воспользоваться 15 законом деформирования
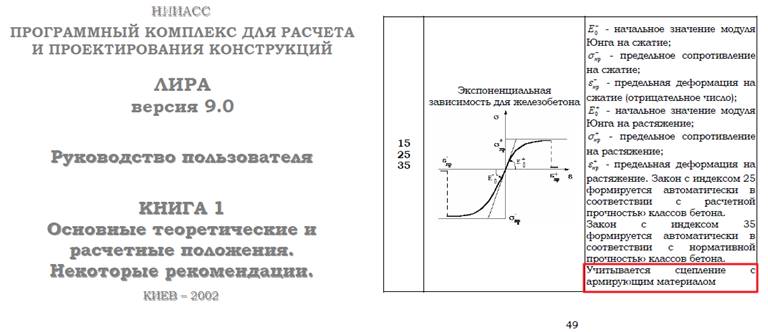
При описании 15, 25 и 35 законов деформирования бетона обязательно следует задать предельные относительные деформации в соответствии с действующими нормами в зависимости от продолжительности действия нагрузки.
Для 11 закона деформирования стали значение предельной деформации при растяжении - 0.025.
Моделирование работы бетона в трещине
При достижении в элементарном слое поперечного сечения элемента напряжения равного Rbt должна возникнуть и раскрыться трещина. На данный момент шаговый процессор для пластинчатых элементов не умеет учитывать данную особенность. Получается, что элементарный слой продолжает пластически деформироваться с модулем упругости Е=1 и «держит» напряжения Rbt.
Это можно исправить следующим образом: ввести новую отсечку на диаграмме, так что при εb→0, Rbt→0 (законы 25, 35) или ввести Rbt→0. Таким образом, можно растянутый бетон полностью выключить из работы.
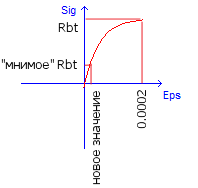
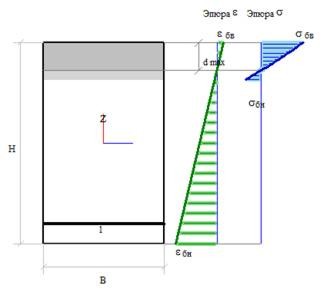
Так, бетон растянутой зоны исключается из работы при относительных деформациях соответствующих σb=Rbt
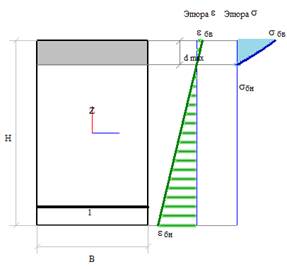
Если задать малую величину предельной деформации на растяжение ε, то можно «выключить» растянутый бетон из работы вовсе
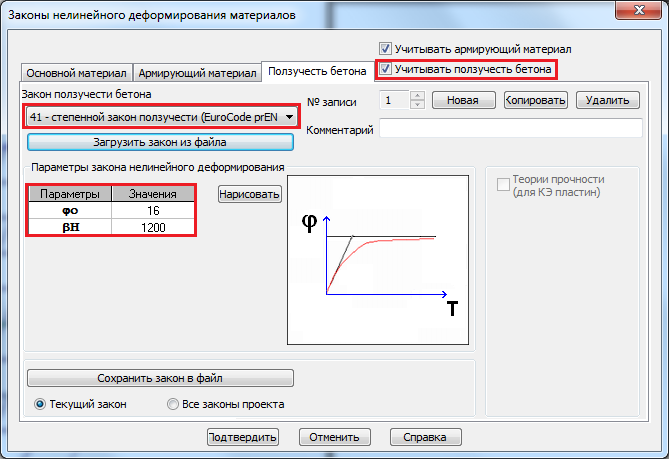
Учет ползучести
Ползучесть можно описать степенным законом в соответствии с Еврокодом EN 1992-1-1 или можно задать произвольный кусочно-линейный закон (44)

Для учета ползучести бетона при физически нелинейном расчете следует установить флажок «Учитывать ползучесть бетона». После этого появляется третья закладка для задания законов ползучести бетона (в соответствии с EN 1992-1-1)