Расчет нормального сечения в КС
При построении геометрии сечений могут быть использованы библиотечные сечения (стандартные сечения и сечения из базы металлических сечений), произвольные контуры, а также полосовые и арматурные включения:
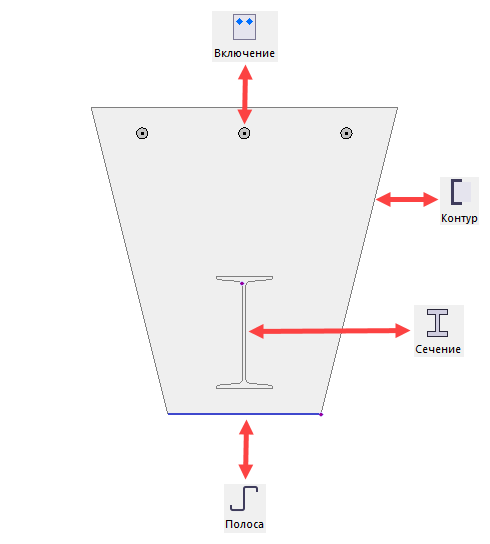
Пример построение многокомпонентного сечения:
Также существует возможность влиять на триангуляцию сечения путем добавления вспомогательных точек.
Для каждого компонента сечения следует назначить материал:
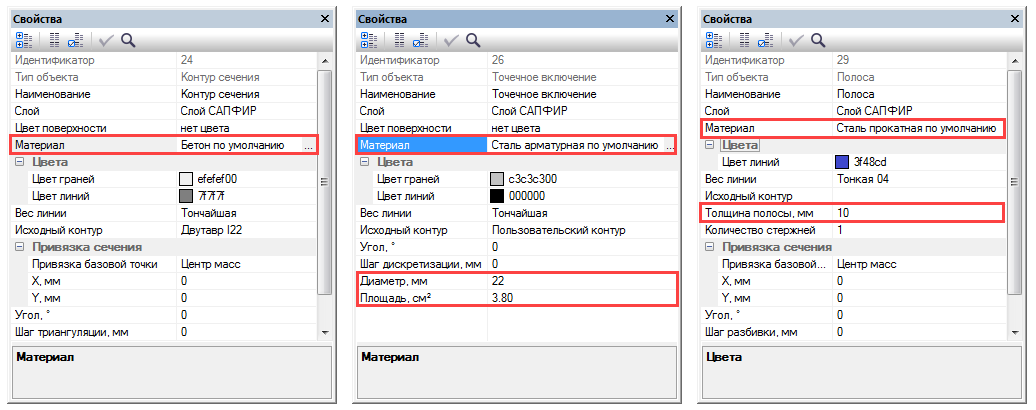
Для арматурных включений дополнительно нужно назначить диаметр/площадь, для полосовых – толщину. Расчет возможен в упругой постановке (приведенное сечение) и нелинейной постановке. Для упругого расчета используется модуль упругости, указанный в характеристиках материала.
При расчете нормального сечения в нелинейной постановке КС+ использует НДМ (нелинейную деформационную модель). Суть расчета по НДМ такова:
- сечение всегда плоское;
- известна зависимость между относительными деформациями и напряжениями для материала σ-ε.
На основе гипотезы плоского сечения известна зависимость между кривизной элемента в рассматриваемом сечении и внешними усилиями. Расчет выполняется итерационным путем – на каждой итерации уточняется жесткость и НДС сечения. Прочность сечения обеспечена если соблюдается равновесие между внешними и внутренними усилиями.
Для расчета в КС+ используются нелинейные материалы со своими диаграммами σ-ε. При назначении материалов существует возможность для бетона использовать готовые диаграммы с экспоненциальной зависимостью σ-ε (21 и 31 законы соответственно с нормативными и расчетными характеристиками прочности):
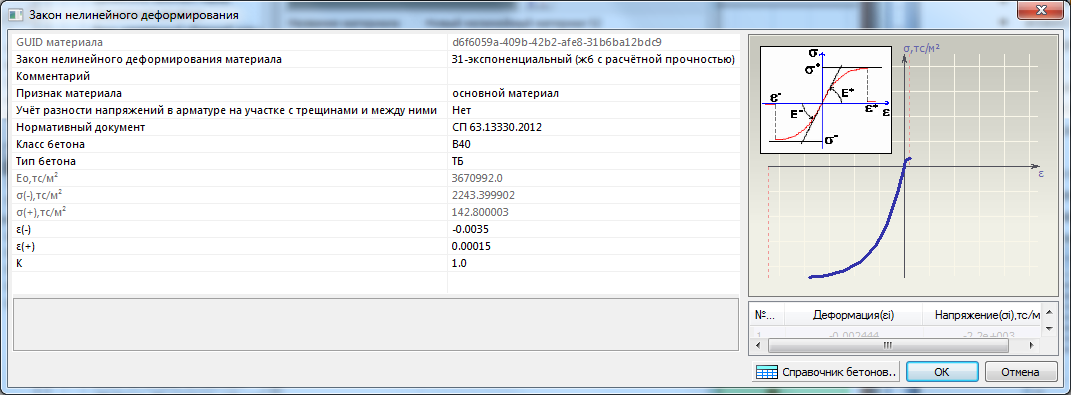
Коэффициенты условий работы бетона можно учитывать заданием коэффициента k отличного от 1 (последняя строка). Предельные относительные деформации по умолчанию соответствуют величинам по СП 63, используемым при прочностном расчете нормального сечения для бетоа классов по прочности на сжатие В60 и ниже.
Также для описания работы бетона и любых других материалов может быть использована кусочно-линейная зависимость (закон №14), где диаграмма σ-ε аппроксимируется ломанной линией.
Пример описания трехлинейной диаграммы для бетона класса В40 σ-ε:
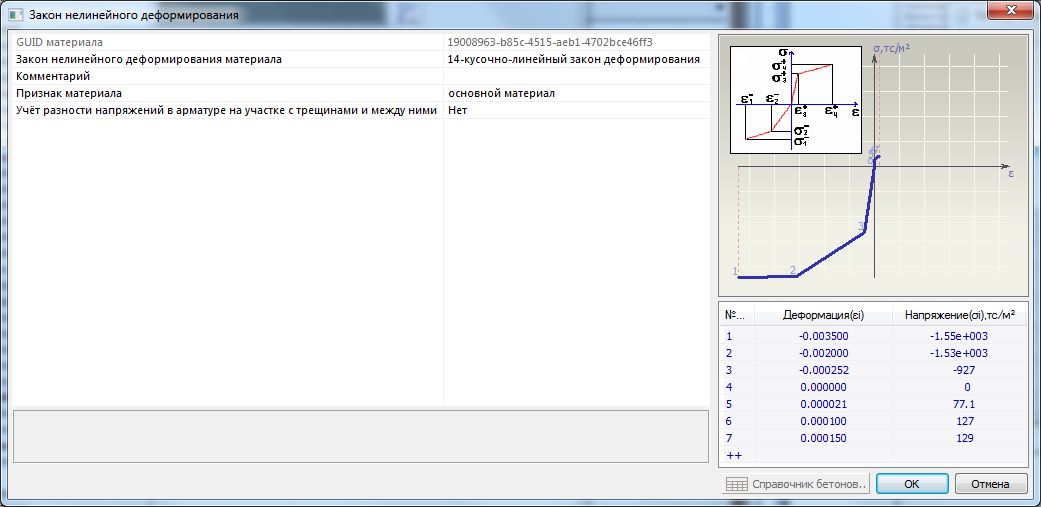
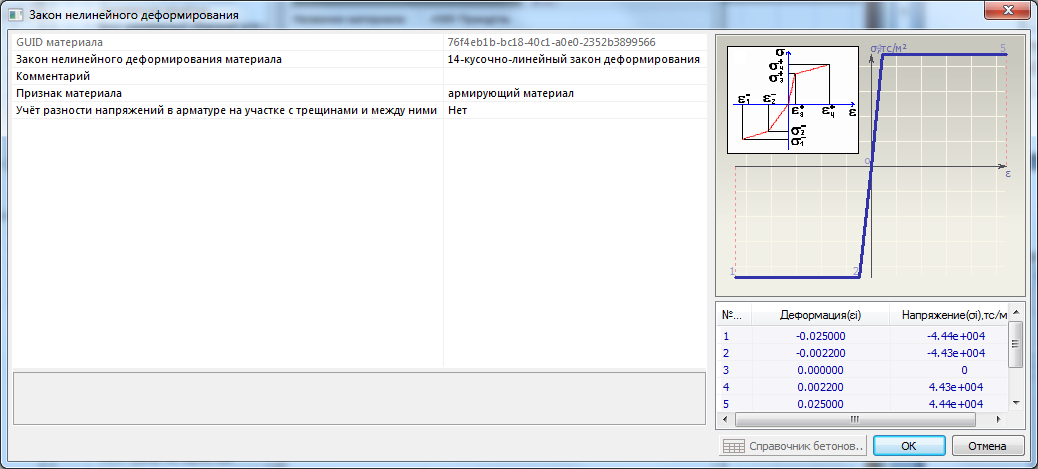
Пример описания диаграммы работы арматуры класса А500 (принята диаграмма Прандтля):
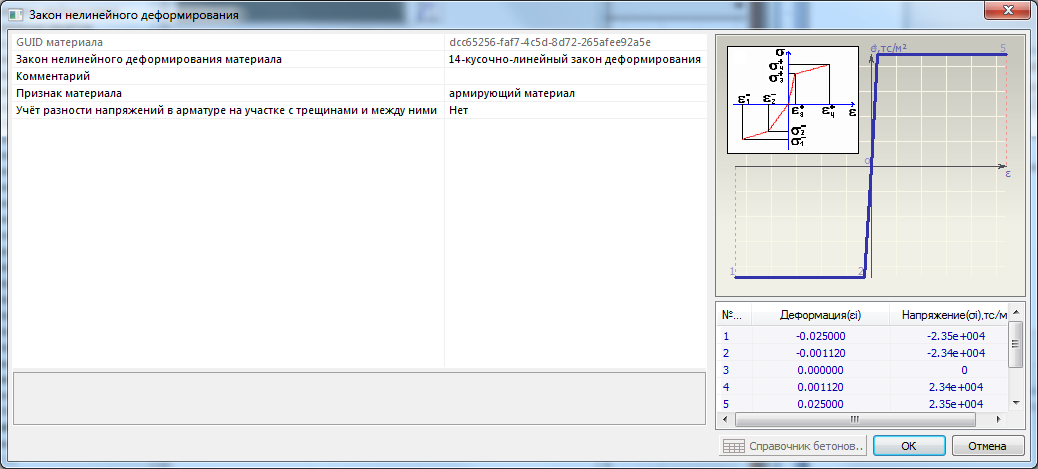
Пример описания диаграммы работы прокатной стали класса С235 (принята диаграмма Прандтля):
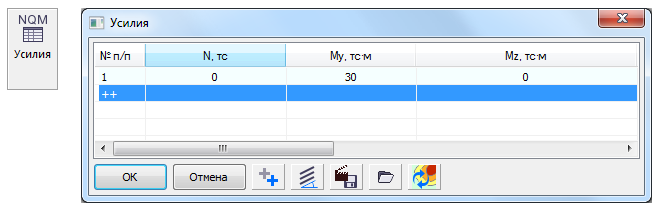
Для нелинейного расчета задаются усилия, действующие на нормальное сечение N, My, Mz:
Пользователь может управлять шагом триангуляции сечения на элементарные треугольники (чем мельче шаг, тем точнее расчет, но тем дольше он выполняется):
По результатам нелинейного расчета можно просматривать характеристики сечения, мозаики/изополя нормальных напряжений, относительных деформаций, секущего модуля упругости, а также усилия в арматурных включениях:

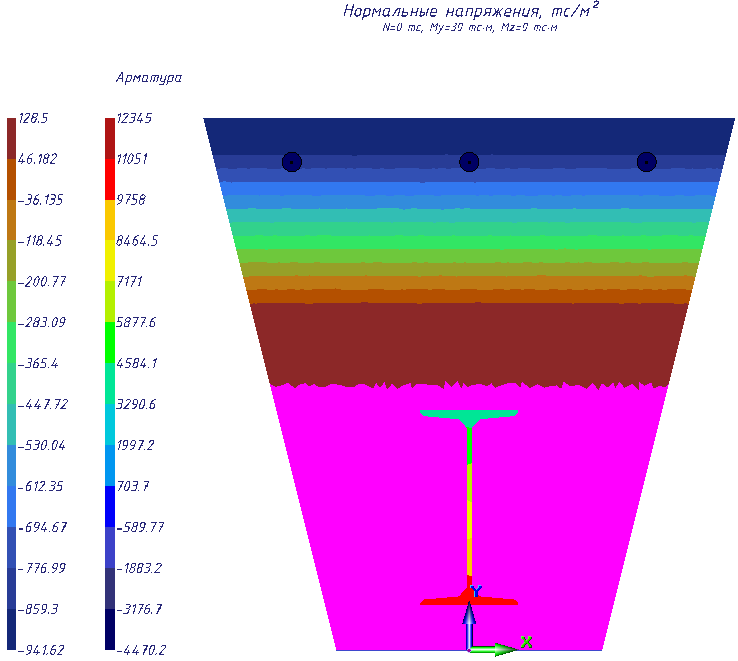
Пример результатов расчета – нормальные напряжения в сечении:
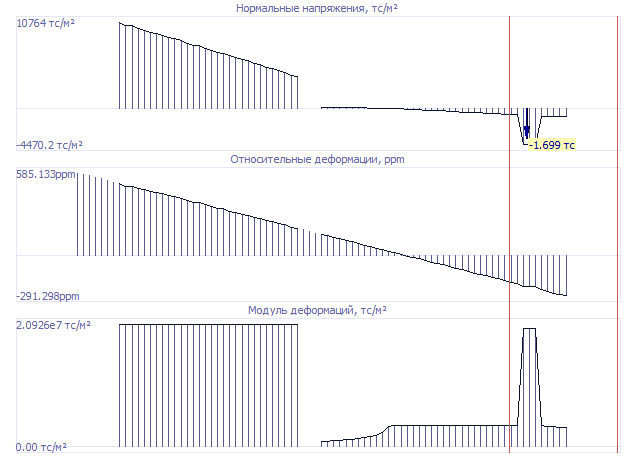
Также можно выводить эпюры по разрезу (А-А). Эпюры σ, ε и Есек в вертикальном сечении, проходящем через ось симметрии сечения:
Эпюры σ, ε и Есек в вертикальном сечении, проходящем на расстоянии 100мм от оси симметрии:
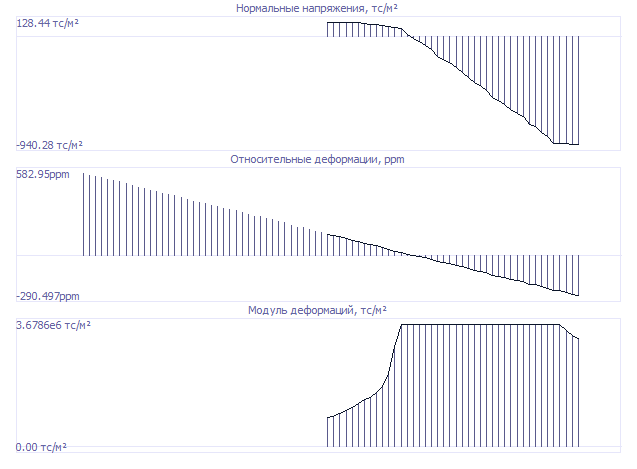
Таблица характеристик сечения:
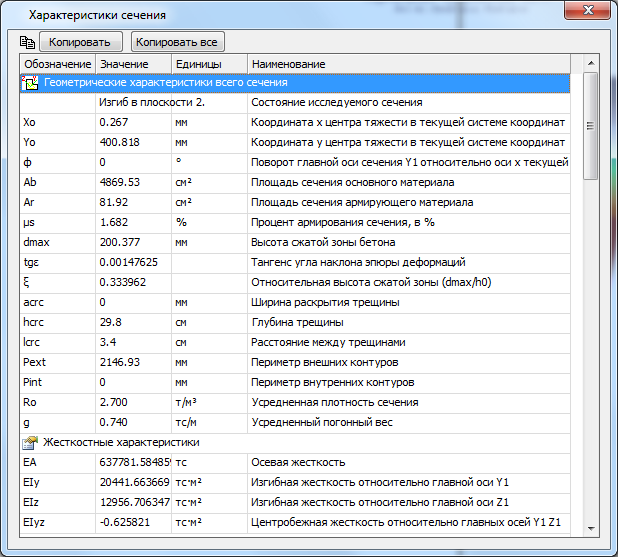
По результатам линейного расчета определяются геометрические характеристики приведенного сечения:
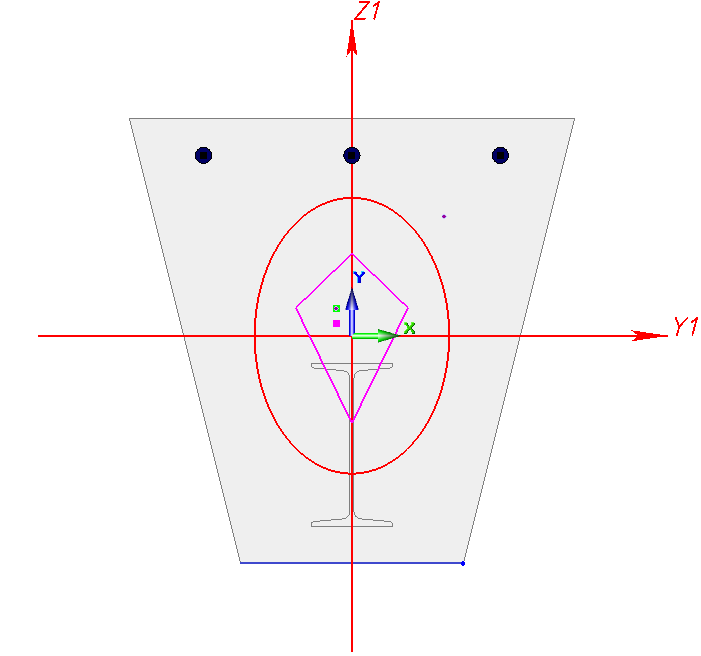
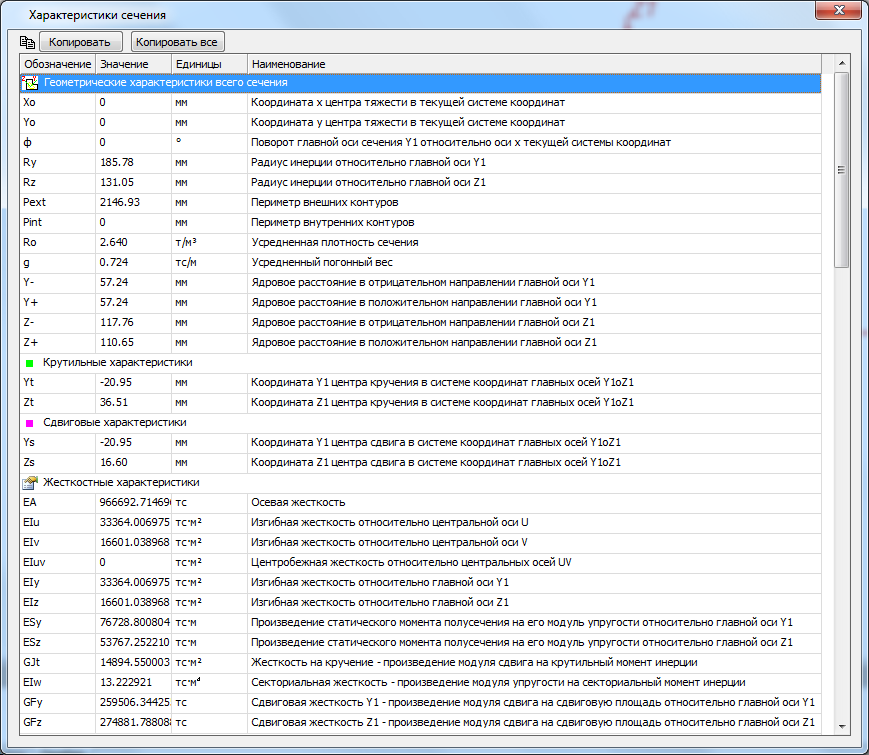
Также возможно вычисление нормальных, касательных, главных и эквивалентных напряжений от всех силовых факторов: N, My, Mz, Mx, B, Qy, Qz (в том числе от бимомента В).
