- ЛИРА-САПР144
- АРМ22
- Алгоритм просчета на продавливание
- Армирование композитной арматурой
- Варианты конструирования
- Информация о сочетаниях при подборе арматуры
- Конструктивный расчет ЖБ сечений
- Коэффициент длительности действия нагрузки
- Материалы для армирования колонны
- Настройки шкалы армирования
- Оболочка, Плита или Стена – что выбрать в типе армирования пластин?
- Осреднение поперечной арматуры в пластинах
- Принятие решения об армировании плит
- Проверка на поперечную силу по п. 8.1.32 СП 63
- Произвольные классы бетона и арматуры
- Просмотр ошибок при подборе арматуры
- Расстановка точек подбора армирования и их ограничения
- Расчет поперечного армирования по модели наклонного сечения
- Результаты подбора арматуры для пластин
- Создание контуров продавливания в Визор и корректировка в САПФИР
- Учет расчетной высоты стен (продольного изгиба) при проверке и подборе армирования
- Числовые мозаики армирования
- Чтение результатов подбора арматуры
- Чтение результатов при расчете на продавливание
- Визор30
- Варианты конструирования
- Документация - примеры расчетов
- Жесткости из МКЭ-расчета и текущие жесткости
- Жесткость КЭ грунта
- Контекстные вкладки
- Контроль приложенных нагрузок
- Копирование свойств узлов и элементов
- Локальные оси узлов
- Нагрузка на ребро пластины
- Нагрузка-штамп и её редактирование
- Объединение перемещений и АЖТ
- Признаки схемы и типы стрежневых КЭ для решения задач в ЛИРА САПР
- Прогибы плит между узлами
- Рампа - вращение образующей
- Расчетные сечения стержней
- Смена типа конечного элемента (КЭ)
- Собственный вес с коэффициентом надёжности
- Согласование осей объемных КЭ
- Согласование осей пластин
- Согласование осей стержней
- Согласование осей стержней для колонн с неточностями монтажа
- Создание объемных КЭ
- Создание одноузловых КЭ
- Сохранение задачи и результатов в ZIP-архив
- Способы применения плитных КЭ при проектировании строительных конструкций
- Строка состояния
- Суммирование нагрузок и центр сил (масс)
- Триангуляция контуров (в САПФИРе)
- Триангуляция контуров с отверстием и простого (в Визоре)
- Удаление нагрузки штамп
- Грунт13
- Взвешивающее действие воды
- Восстановление исходных нагрузок
- Высотная привязка импортированной нагрузки
- Грунтовая подушка
- Импорт данных по скважинам и характеристик грунта
- Импорт нагрузок из DXF
- Итерации для уточнения С1 и жесткостей свай
- Объединение нагрузок
- Определение расчетного сопротивления грунта основания
- Отпор грунта pz при отрыве фундамента
- Предельное напряжение растяжения грунта Rs
- Учет грунта выше подошвы фундамента
- Характеристики грунтов
- Книга отчетов (документатор)4
- Конструктор сечений3
- Настройки10
- Большие иконки для мониторов с высоким разрешением
- ЛИРА-САПР и масштабирование Windows
- Настройка единиц измерения
- Настройка контекстных вкладок
- Настройка языка интерфейса и документирования
- Настройки интерфейса ЛИРА-САПР
- Ограничение загрузки процессора при расчетах
- Рабочие каталоги
- Сохранение, восстановление, перенос и сброс настроек интерфейса
- Хранение связанных файлов и настроек в lir-файлах
- Панельные здания10
- Работа с инструментом стык
- Вертикальный стык стен
- Контактные стыки сборных стен
- Несущая способность горизонтальных стыков
- Платформенный двухсторонний стык
- Платформенный односторонний стык
- Пример расчета жесткости КЭ стыка (платформенный стык при двустороннем опирании плит перекрытия)
- Пример расчета жесткости соединительных элементов в вертикальном стыке стеновых панелей
- Создание КЭ Стыка в ЛИРА-САПР (ВИЗОР) и согласование его осей
- Чтение результатов расчета для КЭ платформенного стыка и соединительных элементов
- Прогрессирующее обрушение2
- Процессор1
- Редактируемый сортамент (РС)4
- Результаты расчетов8
- РСУ, РСН, Метеор15
- Доля длительности в РСУ
- Комбинации РСУ
- Коэффициент надёжности по ответственности здания
- Критерии РСУ
- Несколько таблиц РСУ и РСН в одной задаче
- Объединение временных нагрузок в РСУ
- Работа в системе МЕТЕОР
- Работа с нормативными и расчётными нагрузками
- РСН и РСУ с монтажом
- РСУ для системы МОНТАЖ плюс
- РСУ и РСН при гармоническом воздействии
- РСУ при учете пульсации ветра
- РСУ с дополнительными столбцами
- Сдвиг перемещений и скачки усилий в РСН при динамике
- Учёт комбинаций гололёд и ветровая пульсация
- СТК13
- Конструктивный расчет стальных сечений
- Конструктивный элемент
- Коэффициенты к временным нагрузкам при проверке прогиба
- Локальный расчет элемента схемы
- Невыгодные комбинации по результатам расчёта стальной конструкции
- Проверка местной устойчивости стальных конструкций
- Проверка прогибов стальной балки
- Проверка прогибов стальной балки при косом изгибе
- Расчёт узлов ферм в СТК-САПР
- Расчетные длины стержней
- Сечение одиночный уголок
- Унифицированные усилия в СТК
- Чтение результатов расчёта стальных конструкций
- Теплопроводность3
- Экспорт-импорт данных6
- АРМ22
- САПФИР39
- САПФИР 3D (архитектура, конструкции)31
- API САПФИР
- Аналитический уровень плиты
- Аппроксимация кривых
- Библиотека объектов
- Боковая нагрузка на стены
- Выбор объектов
- Выравнивание аналитической модели плиты по стенам
- Дотягивание
- Импорт поэтажных планов в формате DXF в САПФИР
- Исправление потери нагрузок после проверки
- Комбинации клавиш (Keyboard shortcuts)
- Моделирование капителей в САПФИР
- Моделирование конструкции покрытия зального помещения по серии 1.263.2-4
- Нагрузка на наклонные элементы
- Нанесение текстур
- Настройки для моделирования совместной работы стены и колонны
- Настройки для расчёта ЖБ конструкций
- Настройки нагрузки для приложения на балку
- Пересечение и АЖТ
- Подготовка подложек DXF для построения в САПФИР вручную
- Подготовка подложки DXF для Генератора
- Пользовательская библиотека нодов
- Приложение ветровой нагрузки на стены в САПФИР 2021 R2
- Приложение нагрузки от давления грунта на стены подвала
- Пример назначения типов заданного армирования средствами САПФИР
- Сброс иконок на инструментальных панелях
- Свойства проемов
- Создание наклонных плит и криволинейных поверхностей
- Создание областей различных толщин
- Термовкладыши
- Триангуляция с учетом дополнительных линий
- САПФИР-ЖБК6
- Сапфир падает на видеокартах AMD декабрь 2022
- Следы курсора в Сапфир на видеокартах AMD апрель 2024
- САПФИР 3D (архитектура, конструкции)31
- МОДЕЛИРОВАНИЕ55
- Каркас6
- Нагрузки и воздействия основного сочетания10
- Ветровая средняя (статическая) нагрузка
- Гармоническая нагрузка в вопросах и ответах
- Гармоническая нагрузка, пример расчета балки
- Задание крановых нагрузок в ЛИРА-САПР
- Нагрузка кручение ригеля
- Нагрузка-штамп
- Основы расчета на гармоническое воздействие в ЛИРА-САПР
- Особенности расчета металлических решетчатых башен на ветровую нагрузку
- Особенности расчета многосекционных зданий на ветровую нагрузку (часть 1)
- Особенности расчета многосекционных зданий на ветровую нагрузку (часть 2)
- Нагрузки и воздействия особого сочетания9
- Вклад диафрагм в работу на горизонтальную нагрузку
- Дробная (промежуточная) бальность при сейсмическом воздействии
- Модальные массы
- Модуль 41 — ответ спектр
- Направление сейсмического воздействия
- Определение сейсмической нагрузки на консольные конструкции
- Расчет по СП РК 2.03-30-2017 в ПК ЛИРА-САПР 2017 и младше
- Суммирование форм CQC по формуле 7.18 СП РК 2.03-30-2017
- Учет эффектов случайного кручения при сейсмике
- Нелинейность6
- Особенности МКЭ5
- Узлы сопряжения11
- Моделирование жёсткого защемления балки в стене
- Моделирование перепада отметок плиты перекрытия
- Монолитное ребро плиты – вариант моделирования стержнем таврового сечения
- Монолитное сопряжение стена-колонна
- Сопряжение оболочка-объемник
- Сопряжение плита-колонна
- Сопряжение плита-стена в системе САПФИР-Генератор
- Сопряжение стержень-объемник
- Учет податливости узлов и соединений элементов
- Цилиндрический шарнир
- Шарнир в стержнях
- Фундаменты, основания8
- C1 без модуля грунт
- Задание граничных условий (связей) для фундаментных плит в горизонтальной плоскости
- Моделирование работы свай-стоек
- Положительные напряжения Rz
- Предельно допускаемая нагрузка на сваю
- Расчет подпорной стены
- Увеличение коэффициентов постели в n раз
- Уточнение жесткостей свай (КЭ57) и С1 по методу 2 (Винклер) не сходится
- Админское13
- Локальные и сетевые ключи Guardant. Как работает защита
- Настройка сетевой защиты на ключах Guardant (ЛИРА-САПР)
- Оптимальная конфигурация компьютера для ПК ЛИРА-САПР
- BSOD при установке драйвера Guardant в Windows 11
- KeyUserInfo и прошивка ключа защиты
- Автоматизированная установка и удаление ПК ЛИРА-САПР
- Альтернативная установка ПК ЛИРА-САПР в случае проблем с правами
- Где найти номер ключа
- Дистрибутивы с системными компонентами и без
- Настройка сетевой защиты на ключах HASP (ФОК-Комплекс)
- Перенос настроек интерфейса ЛИРА-САПР между версиями
- Сервер расчетов ЛИРА-САПР
- Установка сервера Guardant 7.0.971 под Linux (2017)
- Для обучения10
- Бесплатные версии ЛИРА-САПР и САПФИР
- ЛИРА-САПР для студентов и самостоятельного изучения
- Методичка ЖБ каркас (РГР-1, МАРХИ)
- Методичка ЖБ оболочки (РГР-2, МАРХИ)
- Подборка бесплатных курсов по ЛИРЕ-САПР
- Пособие по расчету ЖБ плит (Ю.Н. Чудинов)
- Пособие по расчету ЖБ ригеля (Ю.Н. Чудинов)
- Учебные материалы по Лире в свободном доступе
- Книги о программах семейства ЛИРА-САПР в свободном доступе
- Книги от разработчиков ПК ЛИРА-САПР в магазинах
- Альтернативные расчеты1
- Верификация16
- Железобетон1
- Каменные и армокаменные9
- Расчёт кирпичного простенка на косое внецентренное сжатие
- Расчёт кирпичного простенка на косое внецентренное сжатие по нелинейной деформационной модели с подбором армирования
- Расчёт на внецентренное сжатие простенка из газобетонных блоков
- Расчёт на внецентренное сжатие простенка из газобетонных блоков по нелинейной деформационной модели
- Расчёт на внецентренное сжатие простенка из керамического кирпича
- Расчёт на внецентренное сжатие простенка из керамического кирпича по нелинейной деформационной модели
- Расчёт на внецентренное сжатие простенка из силикатного кирпича
- Расчёт на внецентренное сжатие простенка из силикатного кирпича по нелинейной деформационной модели
- Расчёт на внецентренное сжатие с проверкой простенка на центральное сжатие из плоскости изгиба по нелинейной деформационной модели с подбором армирования
- Основания и фундаменты6
Моделирование жёсткого защемления балки в стене
Как правильно смоделировать жёсткое опирание ж.б. балки ж.б. стену? В этой статье будет дан ответ на этот вопрос.
Описание конструкции
Рассмотрим ситуацию, когда ж.б. балка опирается на стену, при этом ось балки параллельна аналитической плоскости стены.
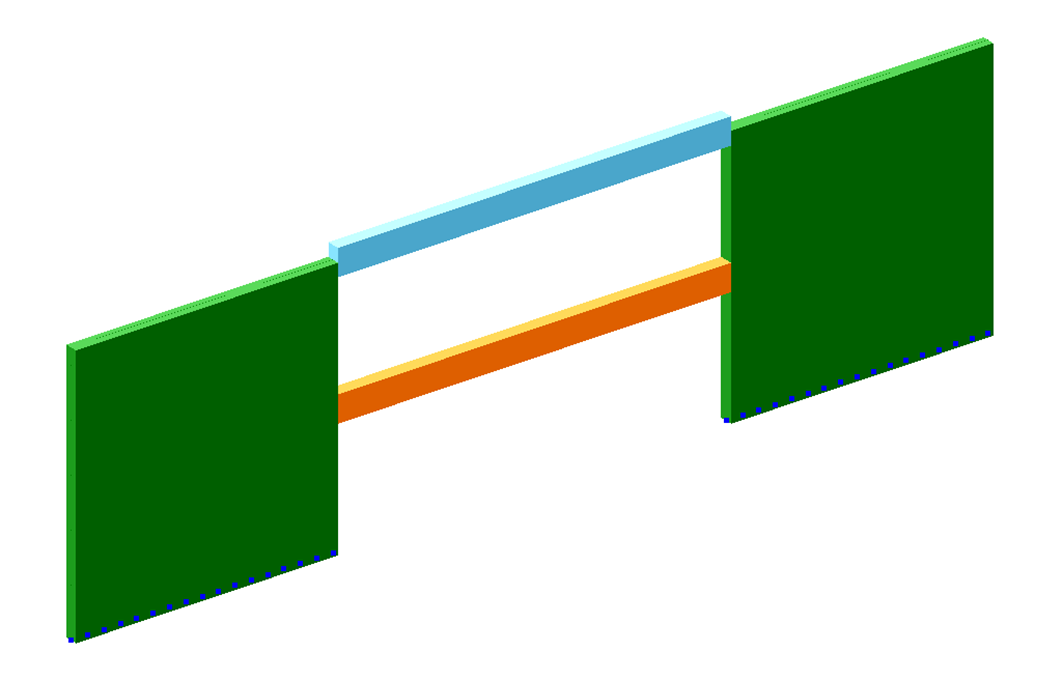
Согласно конструктивному решению, балка должна быть жёстко защемлена в ж.б. стенах.
Моделирование жёсткого опирания балки на стену
Как известно, в ЛИРА САПР, сопряжение двух объектов является жёстким, если в узлах их сопряжения не задано никаких дополнительных условий (шарниры или расшивка с объединением перемещений), однако следует помнить что такое утверждение будет верным при следующих условиях:
- признак схемы допускает передачу изгибающего момента в узлах (2-й,5-й признаки схемы);
- тип КЭ допускает передачу поворота в узлах (стержневые типы 2, 7, 10, пластинчатые – КЭ плит и оболочек)
Поскольку в подавляющем большинстве случаев, при построении расчётных моделей используются стержневые КЭ10 и пластинчатые КЭ-оболочки, то разберём ситуацию жёсткого сопряжения балки со стеной на примере данных КЭ, для чего построим расчётную модель, где смоделируем следующие объекты:
пролет балки 6 м, нагрузка 1 т/м.п.
триангуляция стен сверху вниз: 2х1 м, 1х1 м, 0.5х0.5 м, 0.25х0.25 м, 0.125х0.125 м
эталонное значение опорного момента: q*L^2/12 = 1*6^2/12 = 3 тм
Для моделирования жёсткого защемления балки в стене будем использовать КЭ10 большой жёсткости, который будет заведён в стену на определённую глубину.
Следует отметить, что вышеописанный приём моделирования будет справедлив для режима расчёта схемы с 5 степенями свободы для КЭ-оболочки.
Результаты расчёта
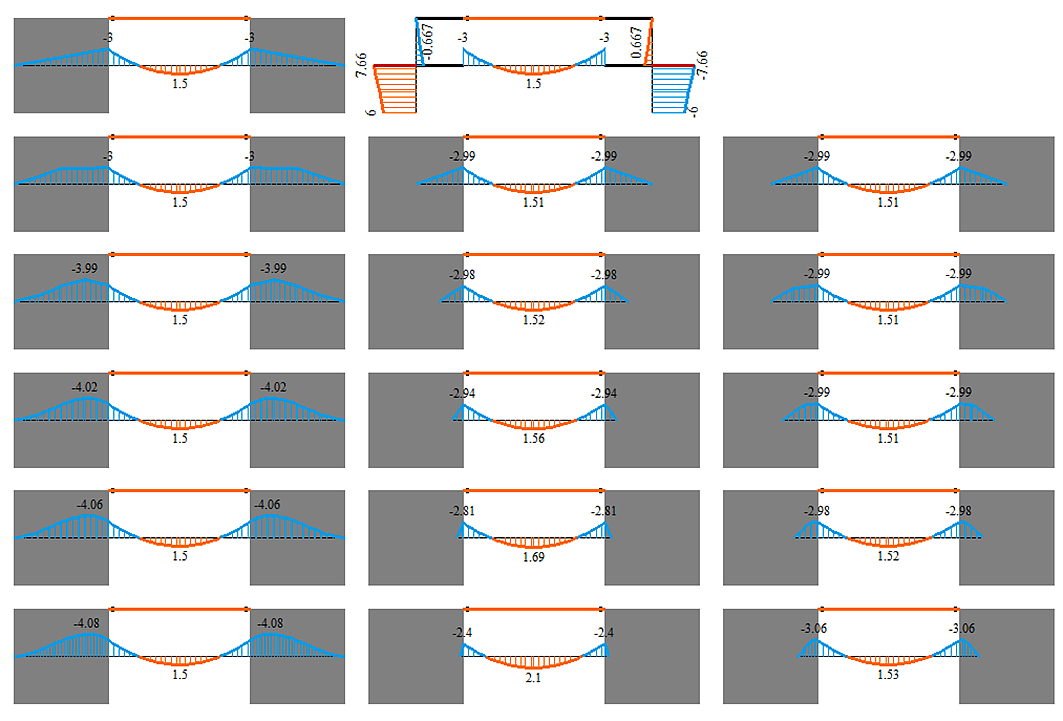
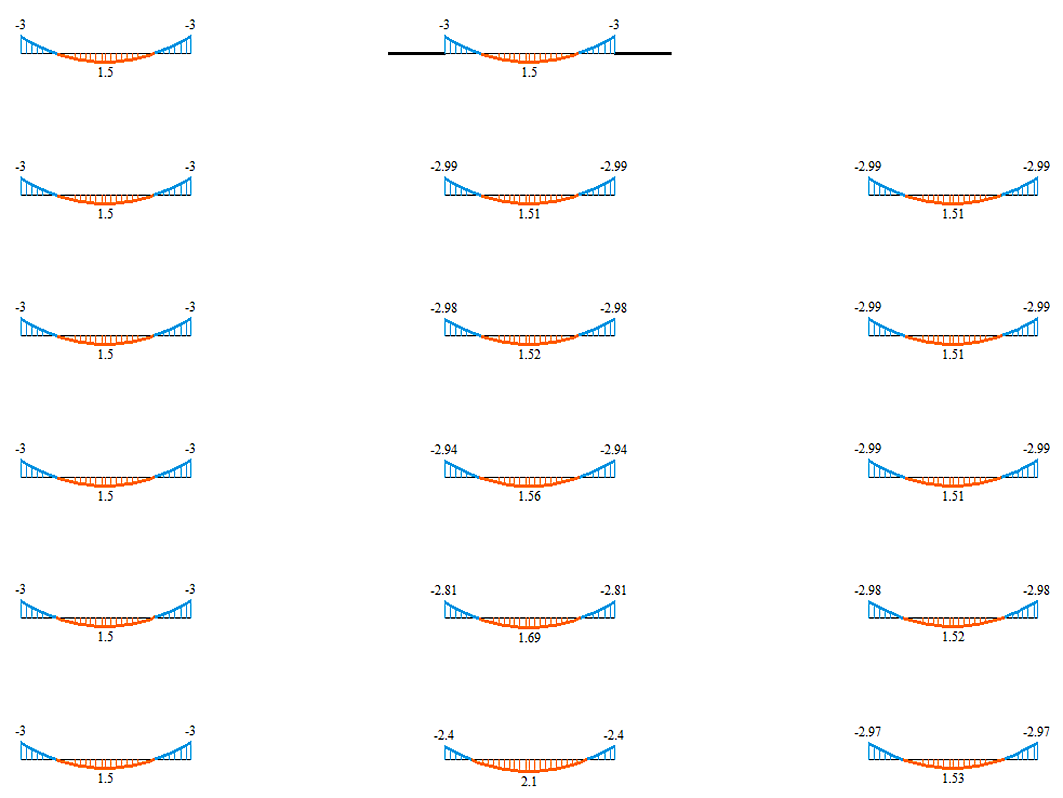
После выполнения статического расчёта, выведем на экран эпюры изгибающих моментов в стержнях.
Вариант слева – жесткий стержень заведен в стены на всю её ширину (при любой триангуляции момент на опоре в балке равен 3 т*м), вариант по центру – на один КЭ (момент на опоре падает со сгущением триангуляции), вариант справа – на разную длину подобранную так, чтобы погрешность не превышала 1%.