Категории

Статей

Основы расчета на гармоническое воздействие в ЛИРА-САПР

Основы расчета на гармоническое воздействие. Реализация в ПК ЛИРА-САПР. Пример расчета

Особенности расчета на гармоническое воздействие

При использовании метода разложения движения по формам собственных колебаний динамические инерционные силы, действующие на систему, представляются в виде синусоидальной и косинусоидальной составляющих S’ и S’’[1]:

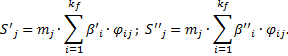
Где

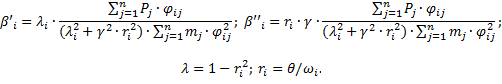
i=(1, 2, 3…kf) – количество рассматриваемых форм колебаний; j=(1, 2, 3…n) – количество степеней свободы;
mj – масса, действующая по направлению j-й степени свободы; φij – ордината i-й формы по направлению j-й степени свободы; Pj – амплитуда гармонической нагрузки по j-й степени свободы; γ – коэффициент неупругого сопротивления материала; θ – частота изменения гармонической нагрузки;
ωi – собственная частота колебаний по i-й форме.

При этом амплитудные (максимальные) значения усилий буду равны:

Где N’и N’’ – обобщенные усилия от синусоидальной и косинусоидальной составляющих S’ и S’’.

В ПК ЛИРА-САПР расчет на гармоническую нагрузку, при использовании разложения по формам собственных колебаний, реализован в модулях 24 и 28. Модуль 24 позволяет выполнять расчет на заданную частоту вынужденного воздействия θ (режим установившихся колебаний), а также с учетом прохождения через резонанс (режим остановка/пуск).

Рис.1. Диалог задания параметров гармонического воздействия по модулю 24

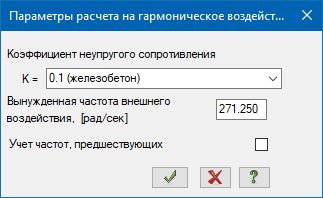
В случае учета предшествующих частот расчет выполняется на заданную частоту θ, а также на значения θi=ωi, где ωi – значения собственных частот колебаний для которых ωi<θ. Т.е. частота вынужденного воздействия приравнивается к собственным частотам системы в диапазоне от ω1 до ωi<θ.

Если учитываются предшествующие частоты (наличие опции «Учет частот, предшествующих»), то в результате получаются несколько вариантов S’ и S’’, последним из которых будет вариант от заданной частоты. Все эти варианты должны быть взаимоисключающими – они не могут возникать одновременно. Это можно учесть в РСУ, назначив для гармонического загружения взаимоисключение (даже если оно одно), при этом все варианты данного загружения будут взаимоисключающими между собой. См. статью https://rflira.ru/kb/91/496/

Модуль 28 позволяет выполнять расчет на заданную частоту вынужденного воздействия θ с учетом частотных зон:

Рис.2. Диалог задания параметров гармонического воздействия по модулю 28

При расчете на гармонические нагрузки должна учитываться возможная погрешность в определении собственных частот, связанная с неточностью исходных данных [2].

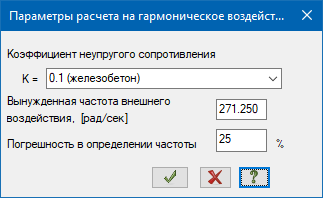
Пример расчета на гармоническое воздействие

Пример 1 (решение представлено в [1] стр. 122-123). Требуется определить динамические силы S’ и S’’ для консоли с двумя массами (m₁=3m, m₂=m) при установившихся колебаниях системы с резонансной частотой θ=ω₂. Коэффициент неупругого сопротивления γ=0.1.

Рис. 3 Расчетная модель и результаты расчета согласно [1]

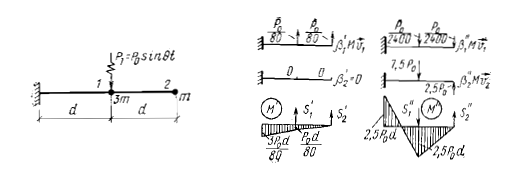
Принимаем что EI=10000 тс*м², вес массы 1 Q₁=3тс, вес массы 2 Q₂=1тс, амплитуда гармонической нагрузки P₀₁=1тс, θ=ω₂=271.25 рад/с, d=2м.

Рис.4. Задание гармонического воздействия в узле

Рис.5. Результаты расчета в ЛИРА-САПР. Формы и частоты колебаний

Рис.6. Результаты расчета в ЛИРА-САПР. Динамические нагрузки. Составляющая S1. Эпюра моментов от составляющей S1

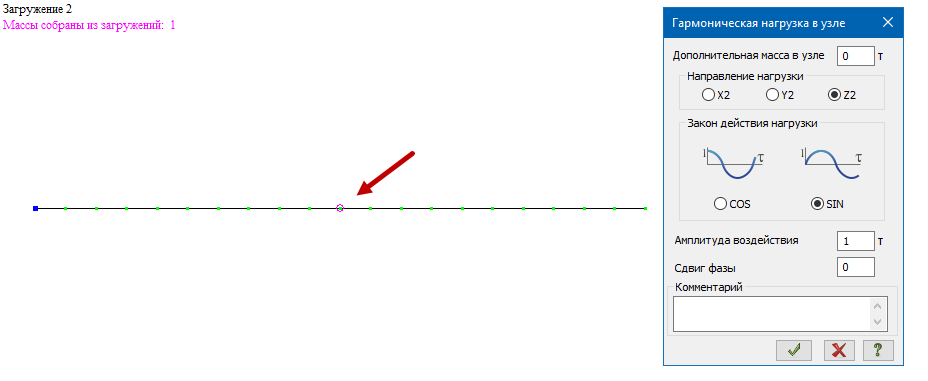
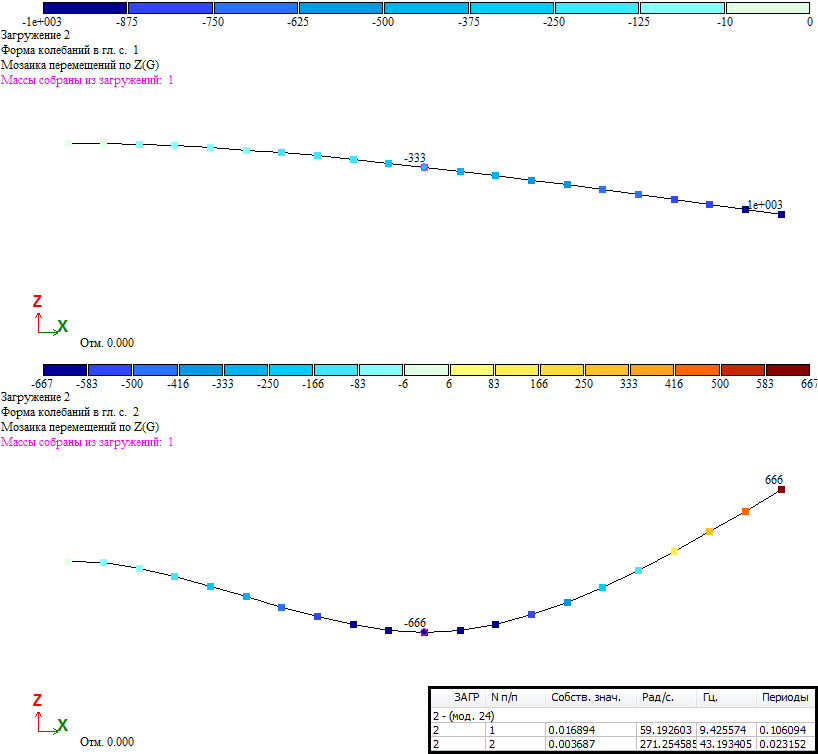
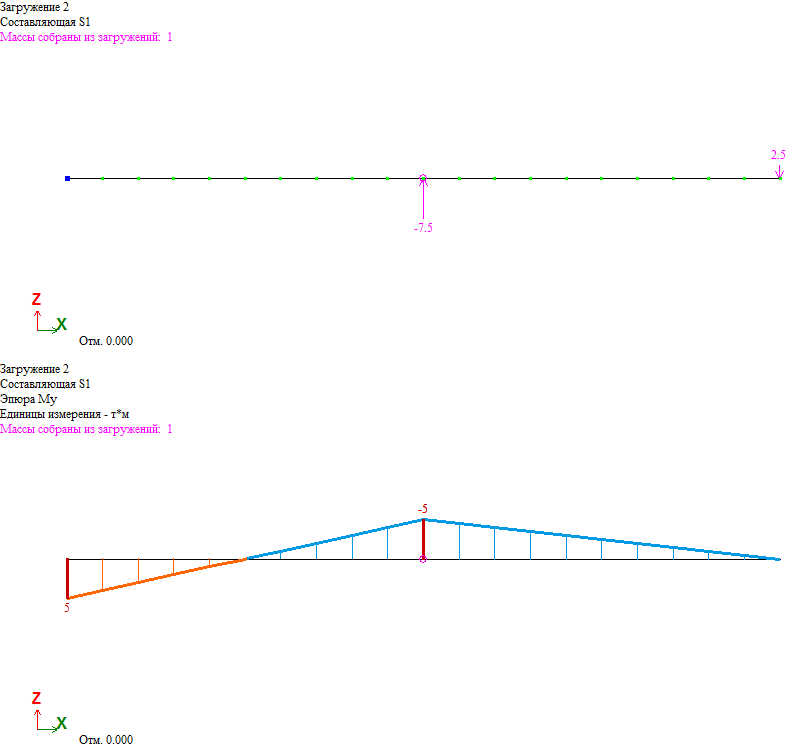
Как видно из результатов расчета (с учетом того, что гармоническая нагрузка является знакопеременной) решение, полученное в ЛИРА-САПР, совпадает с представленным в [1].

Пример 2. Требуется определить динамические силы S’ и S’’ для консоли из примера 1 с учетом того, что к массе m₂ приложена гармоническая нагрузка с амплитудой P₀₂=3тс.

Т.к. масса и жесткость системы не изменились, то ординаты форм колебаний и значения круговых частот такие же, как в примере 1.

Значения узловых масс: m₁=Q₁/g=3/9.807=0.306тс*С²/м; m₂=Q₁/g=1/9.807=0.102тс*С²/м

Ординаты форм колебаний нормированные по 1000: φ₁₁=-333; φ₁₂=-1000; φ₂₁=-666; φ₂₂=666

Промежуточные этапы расчета сводим в таблицы 1 и 2:

Таблица 1

Номер формы	φ_1i/1000	φ_2i/1000	ω_i, рад/с	r_i	λ_i	λ_i²+γ²*r_i²
i=1	-0.333	-1.000	59.193	4.583	-20.0	400.2
i=2	-0.666	0.666	271.26	1.000	0.000	0.010

Таблица 2

Номер формы	P_j*φ_ij		m_j*φ_ij²		β'	β''	m_j*φ_ij
Номер формы	P₁=1	P₂=3	m₁=0.306	m₂=0.102	β'	β''	m₁	m₂
i=1	-0.333	-3	0.034	0.102	1.226	-0.028	-0.102	-0.102
i=2	-0.666	1.998	0.136	0.045	0.000	73.626	-0.204	0.068

Составляющие динамической нагрузки для массы 1 (j=1):

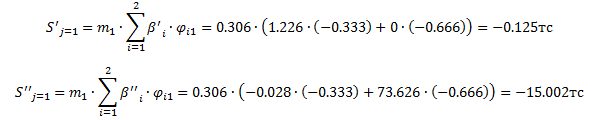
Составляющие динамической нагрузки для массы 2 (j=2):

Схема приложения динамических сил S' и S'':

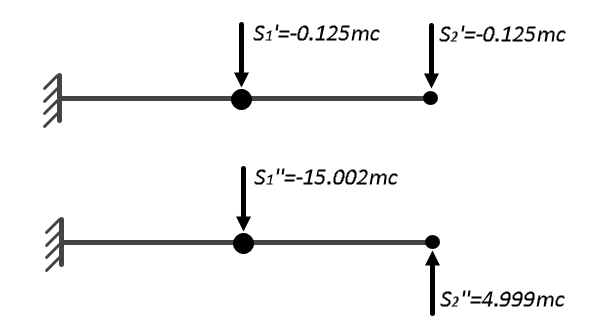
Результат расчета в ЛИРА-САПР:

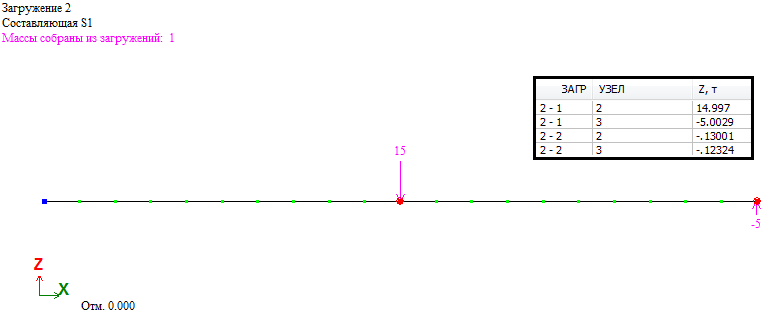
Рис.7. Результаты расчета в ЛИРА-САПР. Динамические нагрузки

Как видно из результатов расчета решение ЛИРА-САПР совпадает с представленным в [1].

Таким образом, ПК ЛИРА-САПР позволяет корректно получать усилия в элементах конструкций при гармоническом воздействии системы сил для всех режимов работы оборудования, а также с учетом погрешностей в определении собственных частот.

При расчете зданий и сооружений на нагрузи от машин и оборудования следует руководствоваться требованиями Инструкции [2].

Используемая литература:

А. Ф. Смирнов, А. В. Александров, Б. Я. Лащеников, Н. Н. Шапошников «Строительная механика. Динамика и устойчивость сооружений». – М.: Стройиздат, 1984.
Инструкция по расчету несущих конструкций промышленных зданий и сооружений на динамические нагрузки. – М.: Стройиздат, 1970.