Учет расчетной высоты стен (продольного изгиба) при проверке и подборе армирования
Что кроется за учётом продольного изгиба?
Рассмотрим колонну с шарнирными неподвижными опорами. На концах колонны приложены изгибающие моменты Me. Колонна загружена осевой силой N. Под действием приложенных моментов Me колонна по длине получает горизонтальные перемещения – выгибается. На выгибах f в колонне появляются дополнительные изгибающие моменты N*f.
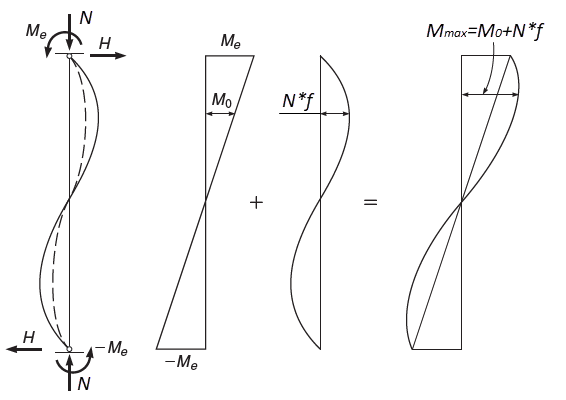
Т.к. железобетон – материал с ярко выраженными нелинейными свойствами, то жёсткость колонны по высоте будет переменной и зависеть от изменения эпюры итогового момента M0+N*f.
При выполнении расчёта с одновременным учётом физической и геометрической нелинейностей можно автоматически получить итоговое распределение моментов по высоте колонны. Однако в подавляющем большинстве случаев расчёт выполняется в упругой постановке при неизменной геометрии конструкции. Соответственно при выполнении конструктивного расчёта необходимо корректировать изгибающие моменты, полученные на основании упругого расчёта.
Учёт влияния продольного изгиба может быть выполнен через корректирующий коэффициент η=Mn/M0, где Мn – момент, полученный в нелинейном расчёте, М0 – момент, полученный в упругом расчёте. Величина коэффициента η в общем случае переменная по длине колонны.
При расчете рамы на действие вертикальных нагрузок, не вызывающих существенных горизонтальных смещений, моменты в опорных сечениях колонн практически не изменяются с переходом на расчет по деформированной схеме, поскольку должны находиться в равновесии с мало изменившимися внешними моментами, приложенными к этим опорам. Тогда для этих сечений η=1.
Если опоры колонны являются смещаемыми в горизонтальном направлении, то моменты в опорных сечениях также увеличиваются.
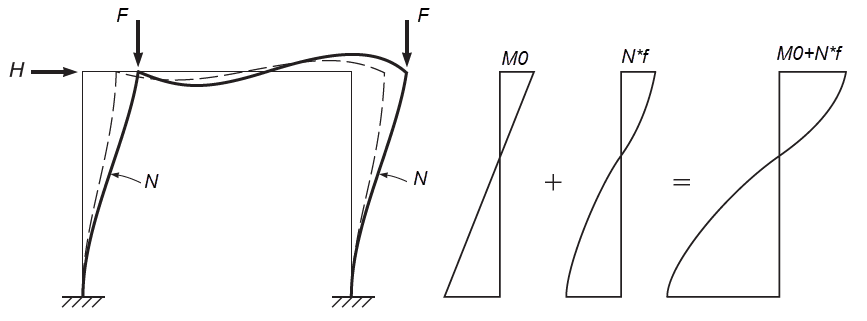
Тогда для всех сечений по длине колонны η>1.
Подход СП 63.13330
Корректировка изгибающих моментов с учётом продольного изгиба согласно СП 63.13330 выполняется на основании метода критических сил [1, 2]. Решается задача Эйлера для стержня на простых опорах.
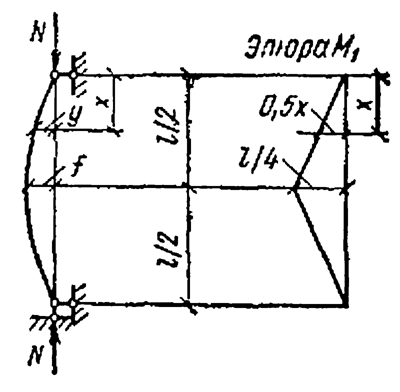
Полный момент в середине пролёта равен:
M=M0+N*f≈M0/(1-N*l^2/π^2*E*I) или M=M0+N*f≈M0/(1-N/Ncr)
где N – действующее в элементе продольное усилие, Ncr – критическая сила. Критическая сила определяется в зависимости от изгибной жёсткости D элемента в предельной стадии работы колонны. При учёте иных условий закрепления, при определении Ncr используется расчётная длина l0 отличная от геометрической l.
Чаще всего при расчёте колонн не выполняется разделение на колонны с несмещаемыми и со смещаемыми опорами. На коэффициент η умножаются изгибающие моменты как в опорных, так и в промежуточных сечениях. Такой подход идёт в запас прочности. Однако согласно последнему абзацу пункта 8.1.15 СП 63.13330.2018 величину коэффициента η можно уточнять:
Методика учёта распределения изгибающих моментов по длине элемента представлена в Пособии к СП 52-101-2003 и книгах по теме [1, 2].

Учёт продольного изгиба для стен при работе их из плоскости
Функция ПК ЛИРА-САПР «Учет расчетной высоты» предназначена для учета продольного изгиба из плоскости пластинчатого конечного элемента.
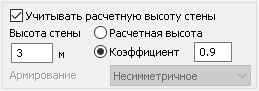
При «учете расчетной высоты» происходит корректировка изгибающего момента My, полученного по результатам расчета, с учетом коэффициента η. При этом согласованные оси для выдачи результатов должны быть направлены таким образом, что местная ось Y1 смотрела вертикально (для стен «высота» определяется направлением согласованной оси Y1).
Решение по учету продольного изгиба принимает пользователь в зависимости от особенностей конструктивного решения здания. Однако применять «в лоб» учёт продольного изгиба для всех пластин не следует. Рассмотрим некоторые примеры.
В перекрёстно-стеновых системах горизонтальные нагрузки воспринимаются за счёт работы стен в их плоскости. Соответственно моменты Mh из плоскости стен отсутствуют. Стены и перекрытия имеют соизмеримые сечения. Т.о. стены имеют податливую на поворот заделку. Значимые горизонтальные смещения стен из плоскости от вертикальных нагрузок в пределах этажа отсутствуют. Таким образом, при расчёте стен в перекрёстно-стеновых системах на действие момента из плоскости с учётом продольного изгиба следует корректировать изгибающий момент, действующий в средней трети по высоте этажа [3]. Для реализации этого подхода в ЛИРА-САПР можно назначить разные материалы КЭ по высоте стены: для опорных сечений без учёта расчётной высоты стены, для остальных – с учётом.
Другой пример – КЭ в углу пересечения стен. Физически данные участки стен не могут свободно выгибаться из плоскости, т.к. стены раскрепляют друг друга по всей высоте этажа.
Ещё один пример – случай действия значительного момента в плоскости пилона, который моделируется пластинчатыми КЭ. При действии значительного изгибающего момента в плоскости пилона будем иметь достаточно большую величину нормальных напряжений в КЭ у одной грани. Учёт продольного изгиба для этих КЭ может привести к их чрезмерному армированию. Такое армирование является следствием того, что за счёт больших сжимающих напряжений получим большую величину коэффициента, учитывающего продольный изгиб и, как следствие, момента, действующего из плоскости пилона. Альтернативой может служить применение стержневых аналогов и конструктивный расчёт пилона по модели нормального сечения.
Используемая литература:
- А.C. Залесов, Э.Н. Кодыш, Л.Л. Лемыш, И.К. Никитин «Расчет железобетонных конструкций по прочности, трещиностойкости и деформациям», 1988.
- Э.Н. Кодыш, И.К. Никитин, Н.Н. Трекин «Расчет железобетонных конструкций из тяжелого бетона по прочности, трещиностойкости и деформациям», 2010.
- Руководство по проектированию конструкций и технологии возведения монолитных бескаркасных зданий. ЦНИИЭП жилища Госгражданстроя, 1982.
