Особенности расчета металлических решетчатых башен на ветровую нагрузку
В статье рассматриваются некоторые аспекты определения ветровых нагрузок на металлические решетчатые башенные конструкции квадратные в плане, а также особенности расчета последних на ветровое воздействие в ПК ЛИРА-САПР
Определение величины ветровой нагрузки
Ветровую нагрузку следует определять как сумму средней wm и пульсационной wp составляющей. Нормативная величина ветровой нагрузки:
Средняя составляющая ветровой нагрузки
Нормативная величина средней составляющей ветровой нагрузки:
где w0 — нормативное значение ветрового давления; k — коэффициент, учитывающий изменение ветрового давления по высоте; с — аэродинамический коэффициент.
Аэродинамический коэффициент для решетчатых башен и пространственных ферм определяется по формуле:
где Cx — аэродинамический коэффициент отдельностоящей плоской решетчатой конструкции:
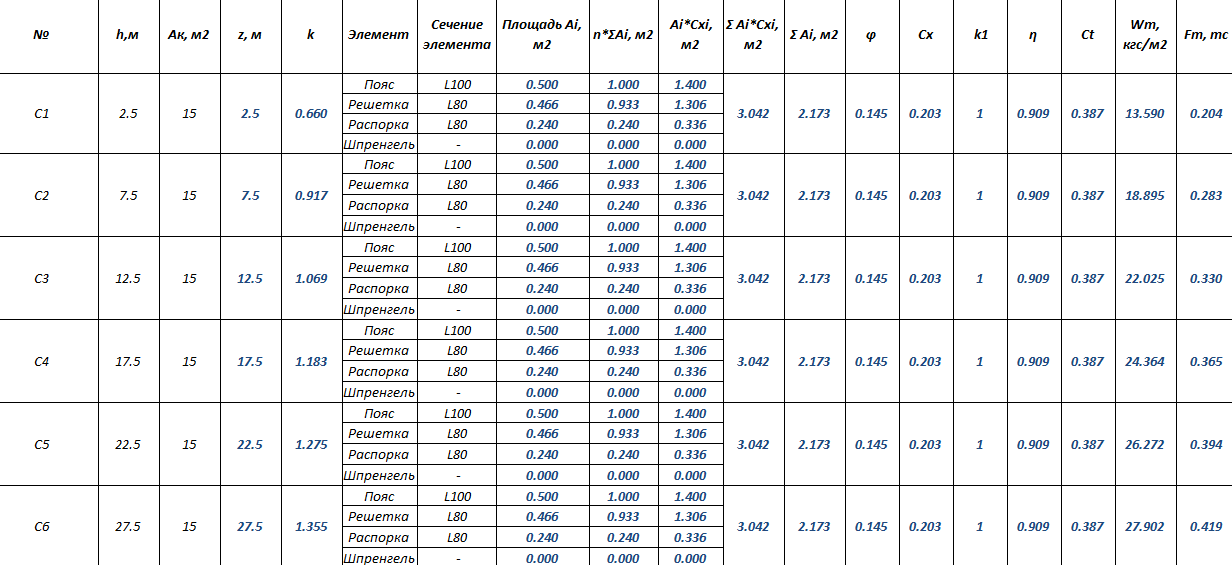
Cxi — аэродинамический коэффициент i-го элемента конструкции; Ai — площадь проекции i-го элемента конструкции; Ak — площадь, ограниченная контуром конструкции.
η — коэффициент, учитывающий давление ветра на подветренную грань. Определяется по табл. В.8 СП 20.13330.2016 в зависимости от относительного расстояния между фермами и коэффициента заполнения ферм.
k1 — коэффициент, зависящий от контура поперечного сечения и направления ветра:
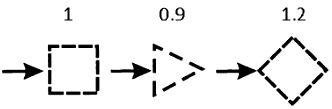
При определении аэродинамического коэффициента решетчатой конструкции Ct принимается, что направление ветра всегда перпендикулярно грани башни:
Таким образом, при определении Ct коэффициент Cx всегда определяется в предположение воздействия ветра на грань, а соответственно ACk — площадь контура грани вне зависимости от угла атаки ветровой нагрузки.
Переход к аэродинамическому коэффициенту Ct при действии ветра на диагональ осуществляется умножением Ct, вычисленного для грани, на коэффициент k1=1.2.
При определении средней составляющей ветровой нагрузки башня разбивается на конечное количество расчетных полей. Далее для каждого расчетного поля определяется площадь, ограниченная контуром Ak; определяется суммарная площадь проекции элементов башни Ai; определяются аэродинамические коэффициенты элементов башни Cxi; определяются коэффициенты Cx, φ, η, k1; определяется аэродинамический коэффициент для решетчатых башен Ct; вычисляется статическая составляющая ветровой нагрузки.
Вычисления удобно выполнять в табличном виде по следующему типу:
Пульсационная составляющая ветровой нагрузки
При определении пульсационной составляющей ветровой нагрузки нужно знать собственные формы и частоты колебаний башни.
Известно, что круговая частота колебаний может быть определена по формуле ω=√(k/m), где k и m – соответственно жесткость и масса. Жесткость зависит от момента инерции башни. Для квадратных в плане башен момент инерции при действии ветра на диагональ и на грань одинаковые:
- момент инерции поперечного сечения башни при площади пояса A и размере башни в плане а относительно оси, параллельной грани (зеленой):
![]()
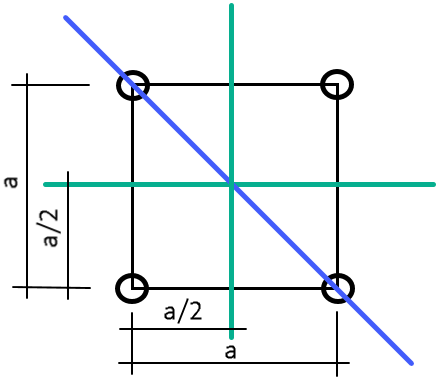
- момент инерции поперечного сечения башни относительно оси, проходящей через диагональ (синей):
![]()
Таким образом, при ветре на диагональ и на грань у квадратной башни одинаковые коэффициент динамичности и ординаты форм колебаний. Поэтому для определения пульсационной составляющей ветровой нагрузки достаточно вычислить частотные характеристики в направлении осей инерции башни, параллельных грани.
В практике проектирования прежних лет пульсационная составляющая ветровой нагрузки определялась только от основной формы колебаний с круговой частотой:
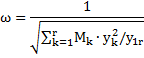
где yk — перемещение точек оси башни при действии единичной силы, приложенной в уровне ее верха; Mk — приведенная к точке масса соответствующего участка башни; y1r — перемещение верха башни от единичной нагрузки.
Пульсационная составляющая ветровой нагрузки в общем случае (динамический анализ) определяется по формуле:
![]()
где m — масса башни на уровне Z, отнесенная к площади поверхности, к которой приложена ветровая нагрузка; ξ — коэффициент динамичности (зависит от линейной частоты колебаний f=ω/2π); y — горизонтальное перемещение на уровне Z по форме собственных колебаний; ψ — коэффициент, определяется по формуле:
![]()
где Mk — масса k-го участка башни; yk — горизонтальное перемещение центра k-го участка (ордината формы колебаний); wpk — равнодействующая пульсационной составляющей ветровой нагрузки на k-й участок:
где ζ — коэффициент пульсаций давления ветра на уровне Z; ν — коэффициент пространственной корреляции пульсаций давления ветра.
Вычисления удобно выполнять в табличном виде по следующему типу:
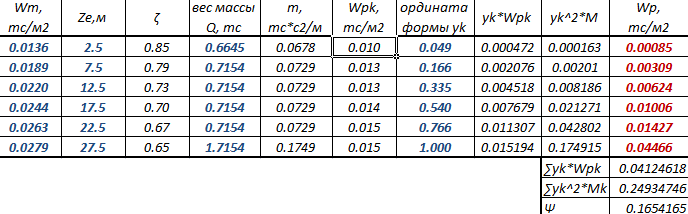
После определения средней (статической) и пульсационной составляющей ветровой нагрузки, определяется полная ветровая нагрузка w=wm+wp. К расчетной модели ветровая нагрузка обычно прикладывается в виде сосредоточенных сил Fi в уровне пересечения поясов с элементами решетки (Fi=w*Ak/n, где n — число узлов).
Далее выполняется определение усилий в элементах башни.
Ветровая нагрузка на металлическую башню должна быть приложена в 2х вариантах — на грань (для определения усилий в решетке) и на диагональ (для определения усилий в поясах).
Усилия в элементах поясов и нагрузки на фундамент квадратной башни при действии ветровой нагрузки определяются от момента Мд и силы Qд – момент и поперечная сила в рассматриваемом горизонтальном сечении башни при действия ветровой нагрузки на диагональ. При этом усилия в поясах, лежащих на диагонали (поперечной/перпендикулярной ветру), равны нулю, а усилия в поясах по направлению ветровой нагрузки равны между собой по абсолютной величине, но разные по знаку
Усилия в элементах решетки определяются при действии ветровой нагрузки от Мг и Qг — момент и поперечная сила в рассматриваемом горизонтальном сечении башни при действия ветровой нагрузки на грань.
Пример расчета башни на полную ветровую нагрузку определенную «ручным» способом
Рассмотрим башню с параллельными поясами высотой 30м. Размер в плане а=3х3м.
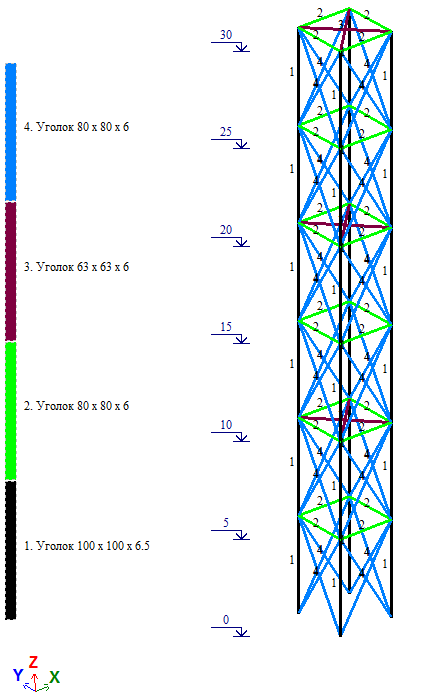
Нагрузки на башню:
- собственный вес;
- вес оборудования 1тс в уровне верха башни (0.25тс в узел);
- ветер полный на грань;
- ветер полный на диагональ.
Ветровая нагрузка прикладывается как узловая в уровне верха расчетного поля. Величина полной ветровой нагрузки складывается из статической и пульсационной составляющих. Рассматривается 6 расчетных полей по высоте.
Табл. 1
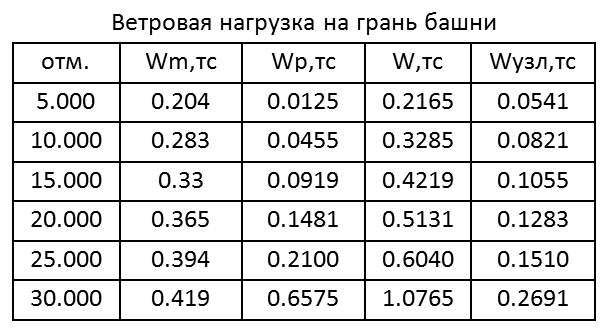
Табл. 2
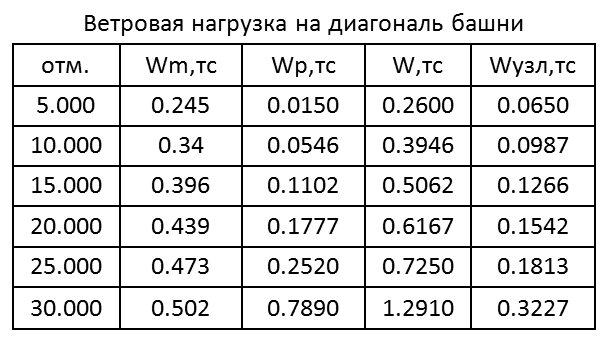
Усилия в элементах башни при действии ветровой нагрузки на грань.
Проверка. Общий момент в основании башни Мг=∑Wiг*Zi=68.35тс*м. Нагрузка на фундамент F=(Мг/а)/2=(68.35/3)/2=11.39тс
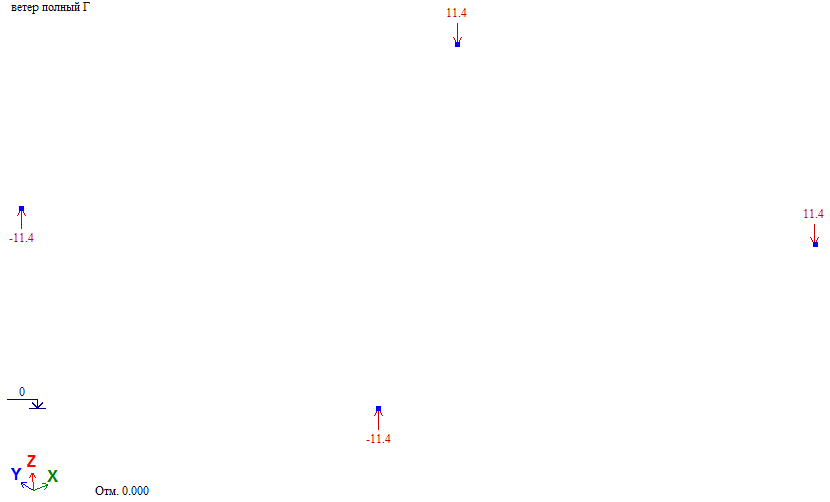
Как видно результаты программного и «ручного» определения нагрузок на фундаменты сходятся.
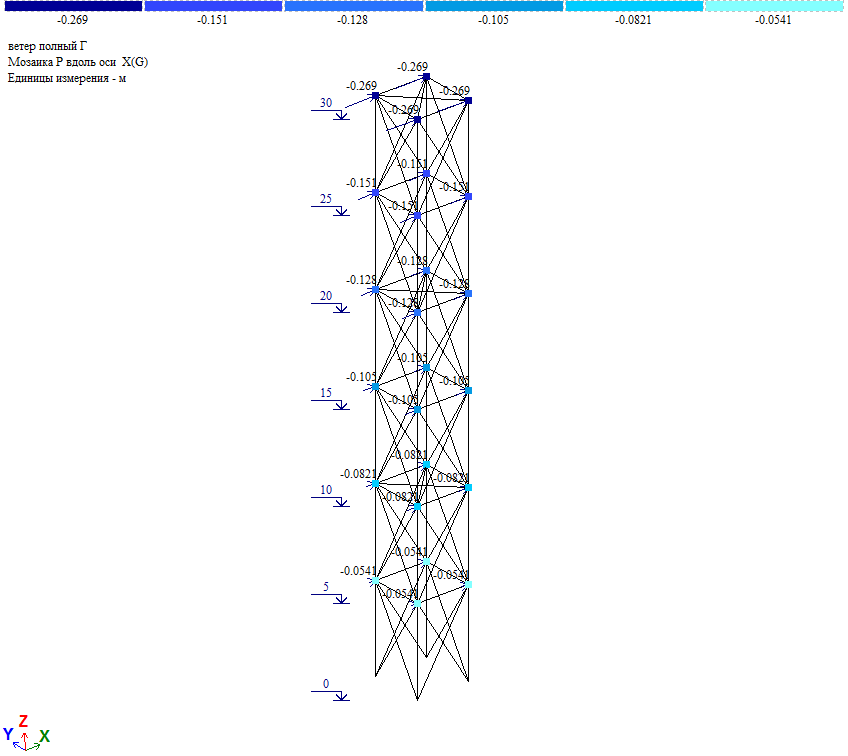
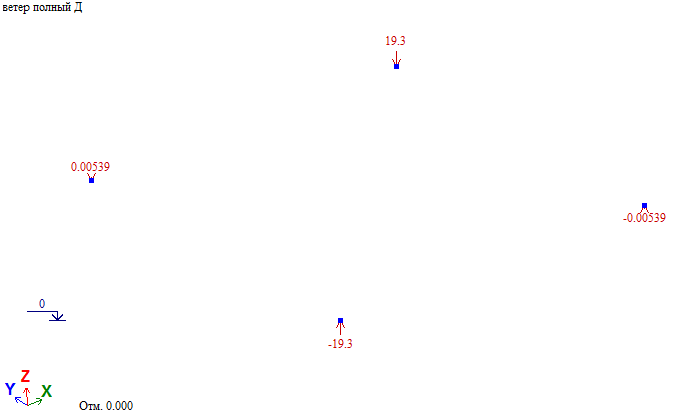
Усилия в элементах башни при действии ветровой нагрузки на диагональ.
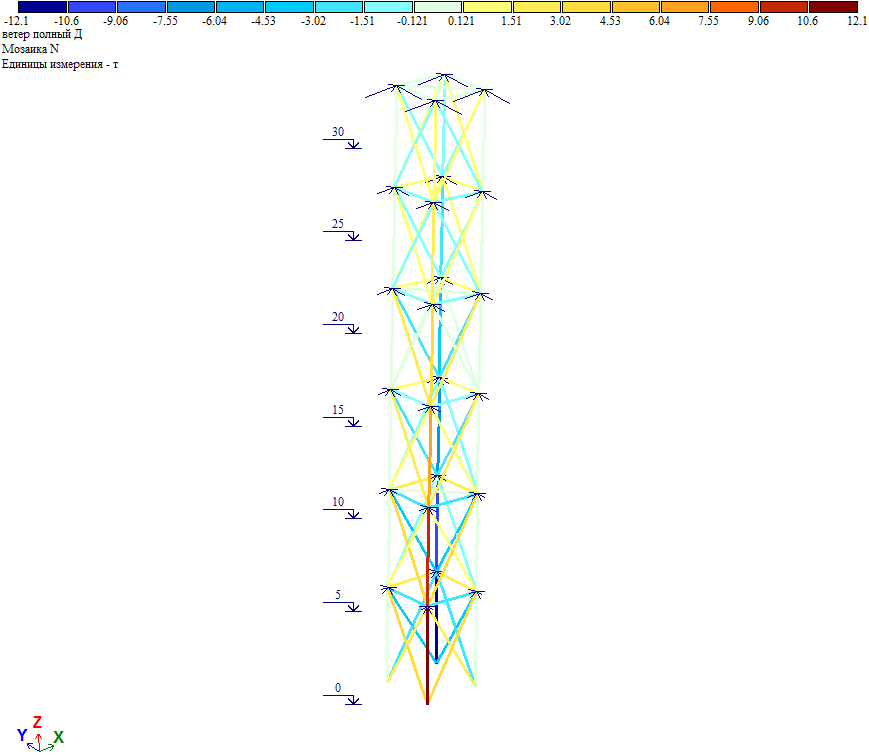
Проверка. Общий момент в основании башни Мд=∑Wiд*Zi=82тс*м. Нагрузка на фундамент F=(Мд/а*√2)=(82/3*1.414)=19.33тс
Нагрузки на фрагмент в основании башни:
Моделирование воздействия ветра в ЛИРА-САПР
При конечноэлементном моделировании башня представляется пространственной фермой. Т.к. жесткость и масса конструкции величины не зависимые от внешней нагрузки, то при определении собственных форм и частот колебаний для разных пульсационных загружений имеет место случай кратных форм колебаний, т.е. форм с одинаковой частотой.
Если частотное уравнение имеет кратные формы, условие ортогональности форм (вдоль граней башни, в данном случае вдоль глобальных осей Х и У) не справедливо. В этом случае существует целое семейство векторов, любая пара из которых может служить собственными векторами для кратных частот. Эта пара будет ортогональна друг другу, но произвольно повернута вокруг вертикально оси башни:
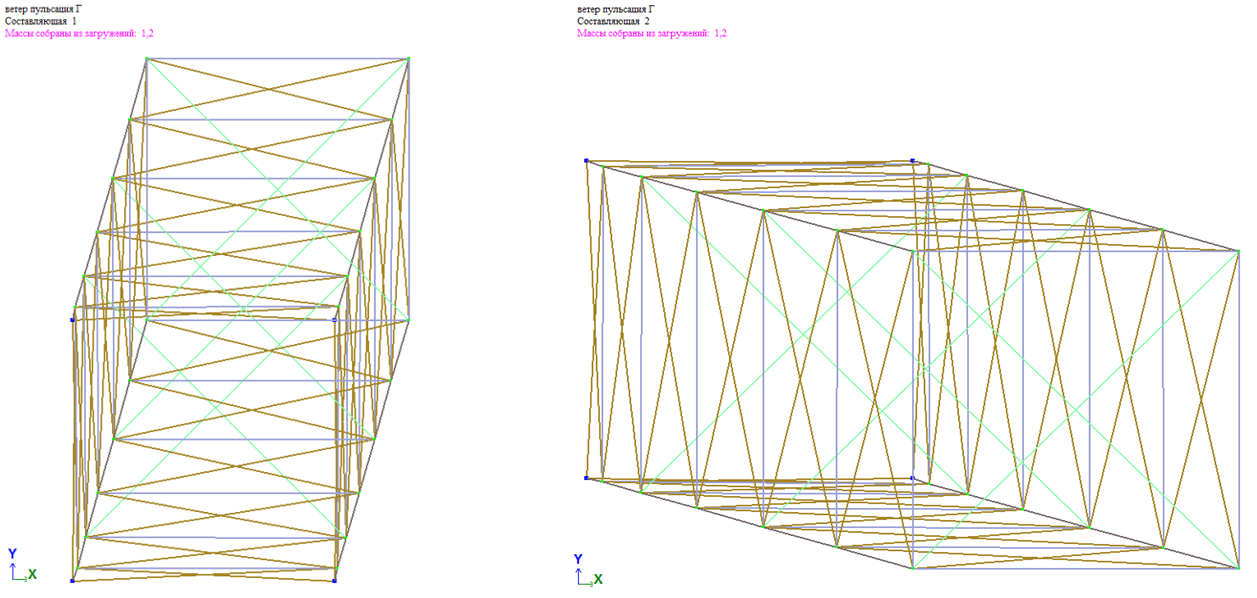
Т.к. ординаты форм колебаний учитываются при определении величины пульсационной составляющей ветровой нагрузки, то в случае кратных форм последняя будет зависеть от угла поворота перемещения по кратным формам относительно главных осей сооружения. Если учесть, что угол поворота кратных форм величина случайная, то прогнозировать правильность результатов сложно. В данном случае возможно как уменьшение, так и увеличения вклада ветровой пульсации в усилия в элементах схемы.
Правильный результат будет получен в случае совпадения направления перемещений по одной из кратных форм с направлением ветровой нагрузки.
Для борьбы с кратными формами колебаний применяют разные подходы. Наиболее распространенные из них – изменение геометрии (жесткости) или масс. К примеру, в справке к ПК Abaqus написано:
| «In cases with repeated eigenvalues and eigenvectors, the modal summation results must be interpreted with care. You should add insignificant mass to the structure or perturb the symmetric geometry such that the eigenvalues become unique» | «В случаях с повторяющимися собственными значениями и собственными векторами результаты модального суммирования должны интерпретироваться с осторожностью. Вы должны добавить несущественную массу к конструкции или нарушить симметричную геометрию, чтобы собственные значения стали уникальными» |
При изменении геометрии башня создается прямоугольного сечения с размерами а и k*a (k принимается 1.01-1.05). При изменении масс по одному из направлений прикладываются дополнительные массы (0.01-0.05 от общей массы сооружения по данному направлению).
В ЛИРА-САПР версии 2018 появился новый инструмент Суммирование кратных форм. В случае ветровой пульсации направление итоговой формы колебаний принимается по направлению статической составляющей ветровой нагрузки. Так при ветре, заданном на грань, суммарная форма перемещений также будет на грань. При направлении ветра на диагональ, заданном через 2 составляющие вдоль осей X и Y, итоговое направление формы перемещений будет по направлению равнодействующей, т.е. тоже на диагональ.
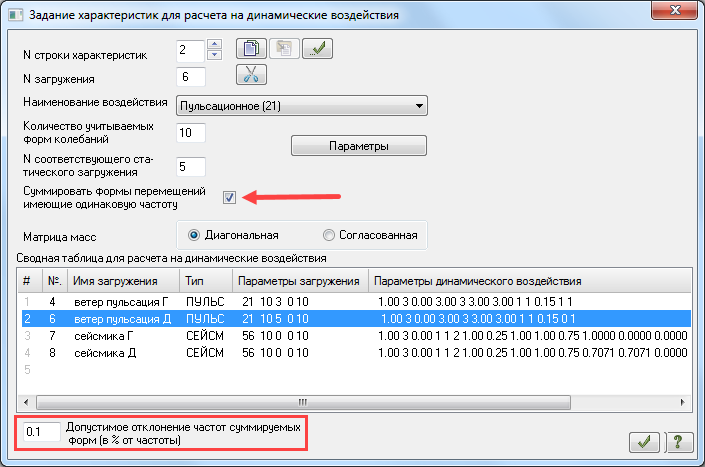
Ниже будут показаны варианты расчета башни на действие пульсационной составляющей ветровой нагрузки с учетом суммирования по формам колебаний и без него. Сравниваться будет НДС схемы при определении величины ветровой пульсации «ручным» способом (см. выше) и программно.
Суммирование кратных форм
К башне, описанной выше, прикладывается статическая составляющая ветровой нагрузки. Пульсационная составляющая определяется программно.
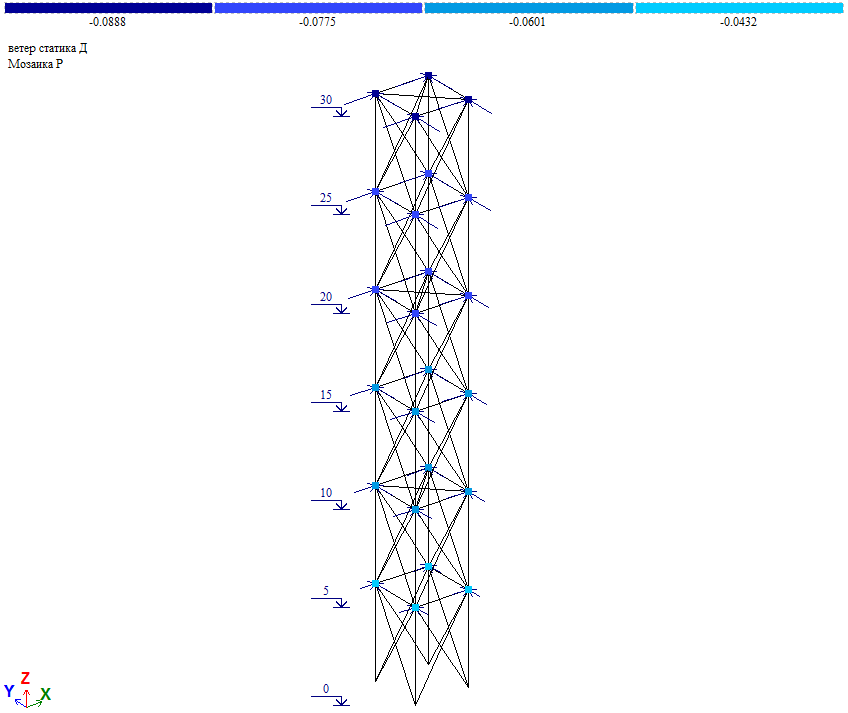
Ветер на грань.
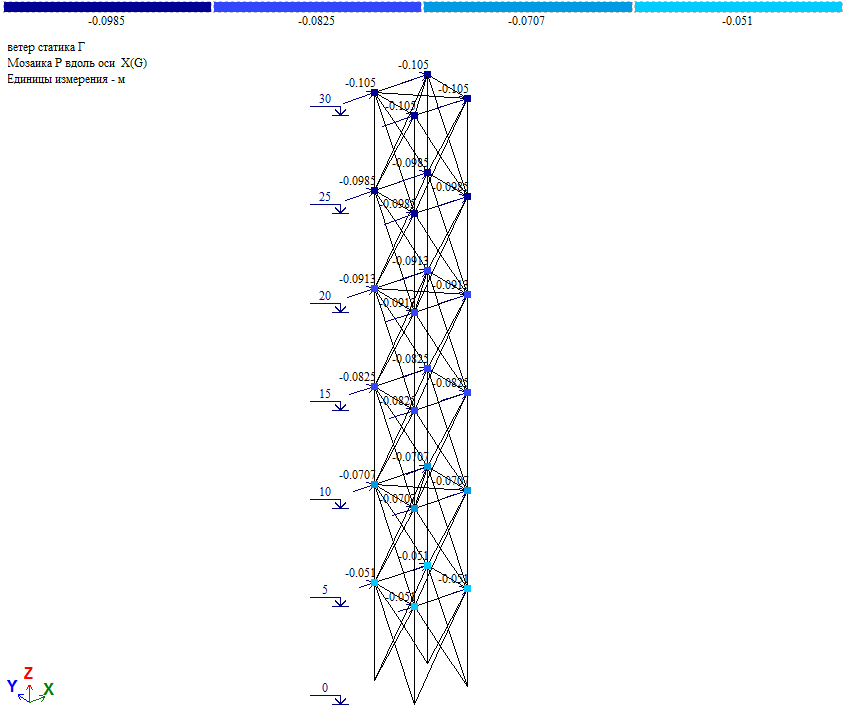
Величина узловой нагрузки Wm/4 (Wm см. таблицу 2).
Пульсационная составляющая по результатам расчета:
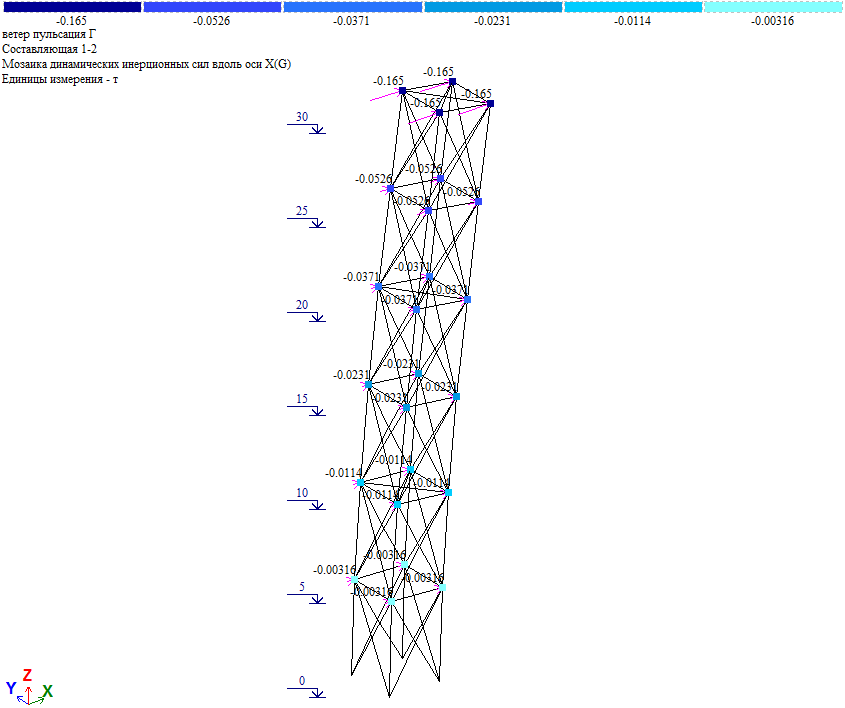
Пульсационная составляющая в уровне отм. +30.000 Wp=0.165*4=0.66тс, что близко к величине нагрузки в таблице 1 (Wp=0.6575тс). Т.е. результаты «ручного» и программного расчета совпадают.
Усилия в элементах башни от полной ветровой нагрузки на грань (получено через РСН):
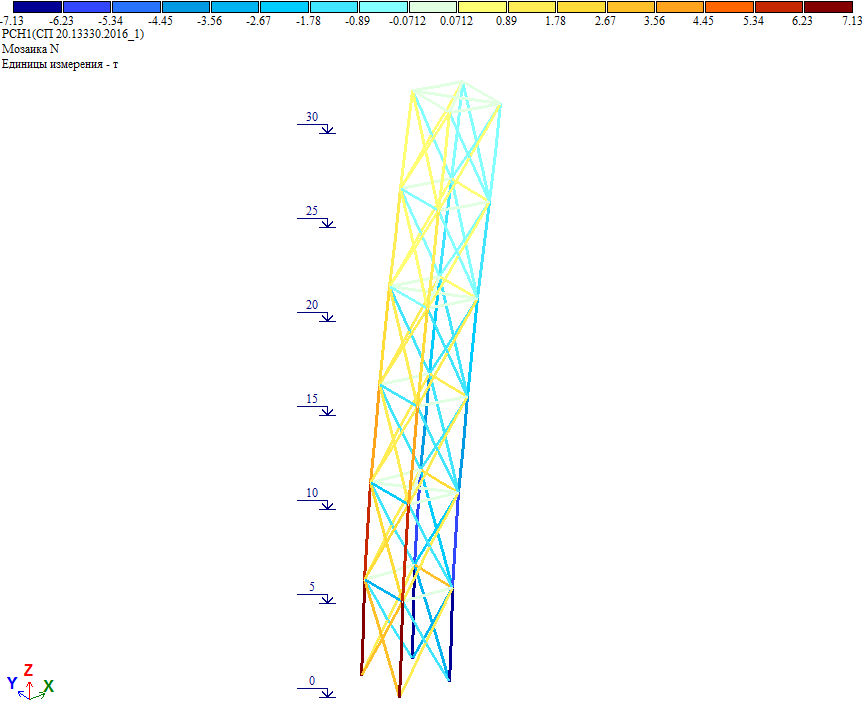
Как видно, усилия совпадают с результатом расчета, где к башне приложена полная ветровая нагрузка на грань, определенная «вручную» и приложенная единой нагрузкой.
Ветер на диагональ.
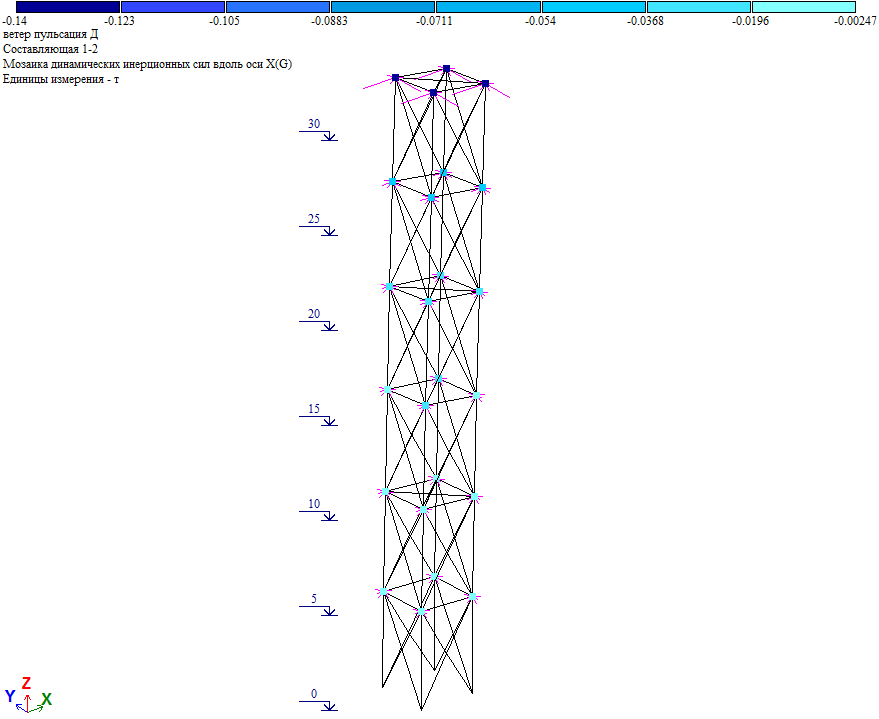
Пульсационная составляющая в уровне отм. +30.000 Wp=Wpx/cos45⁰=(0.14*4)/0.7071=0.792тс, что близко к величине нагрузки в таблице 2 (Wp=0.789тс). Т.е. результаты «ручного» и программного расчета совпадают.
Усилия в элементах башни от полной ветровой нагрузки на диагональ:
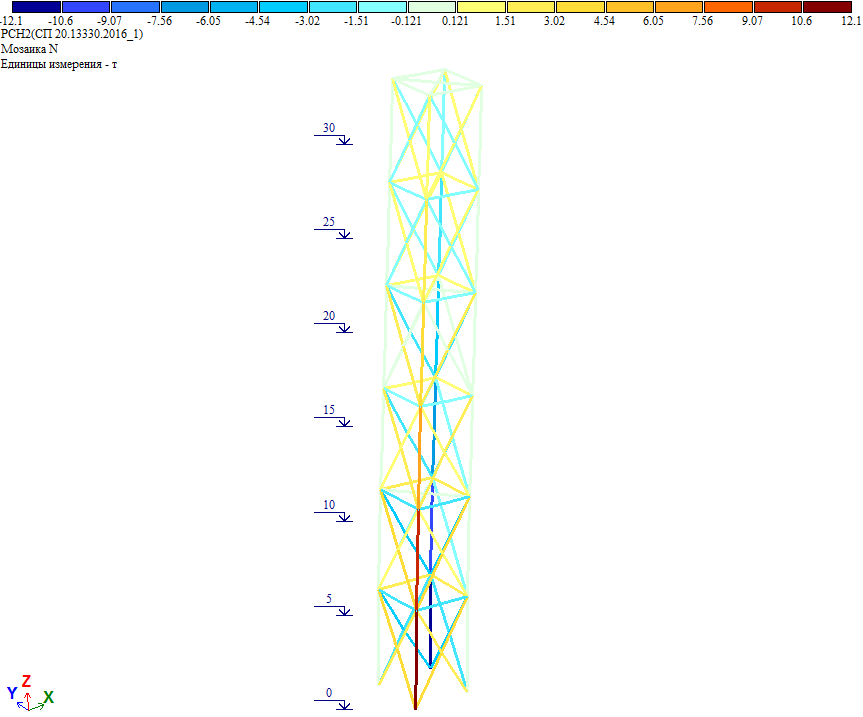
Как видно, усилия совпадают с результатом расчета, где к башне приложена полная ветровая нагрузка на диагональ.
«Управление» кратными формами
При расчете башни без использования функции «Суммировать формы перемещений» кратными формами колебаний следует управлять, чтобы получить ожидаемый результат. Так при ветре на грань следует задать дополнительные веса масс по направлению воздействия ветровой нагрузки:
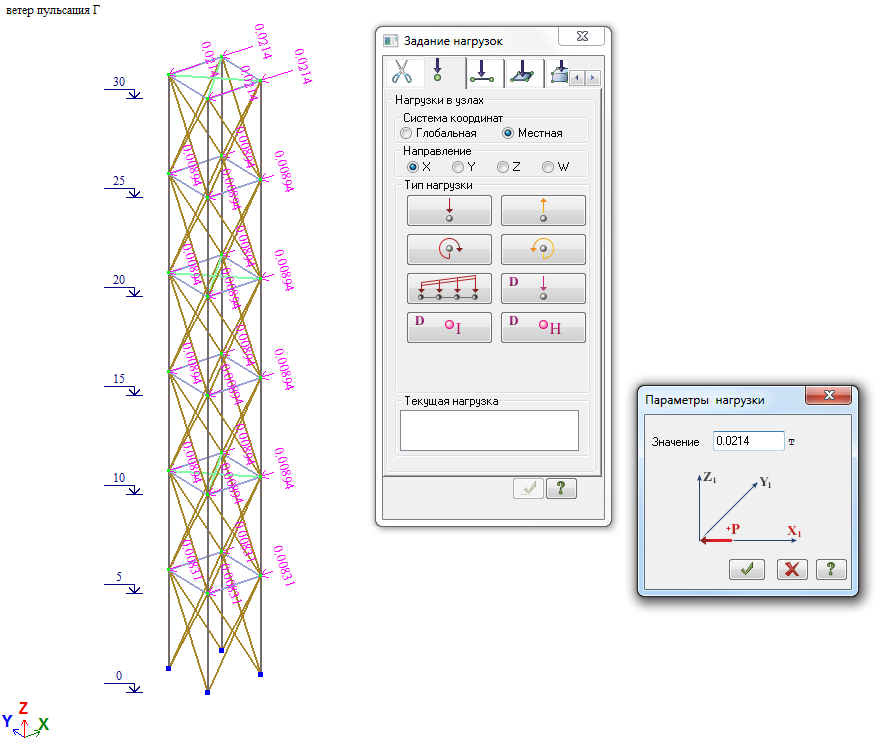
Величина дополнительных весов масс принимается 0.01-0.05 от общего веса массы сооружения по данному направлению.
В примере выше для каждого уровня принята величина дополнительной массы, пропорциональная массе сооружения на данном уровне.
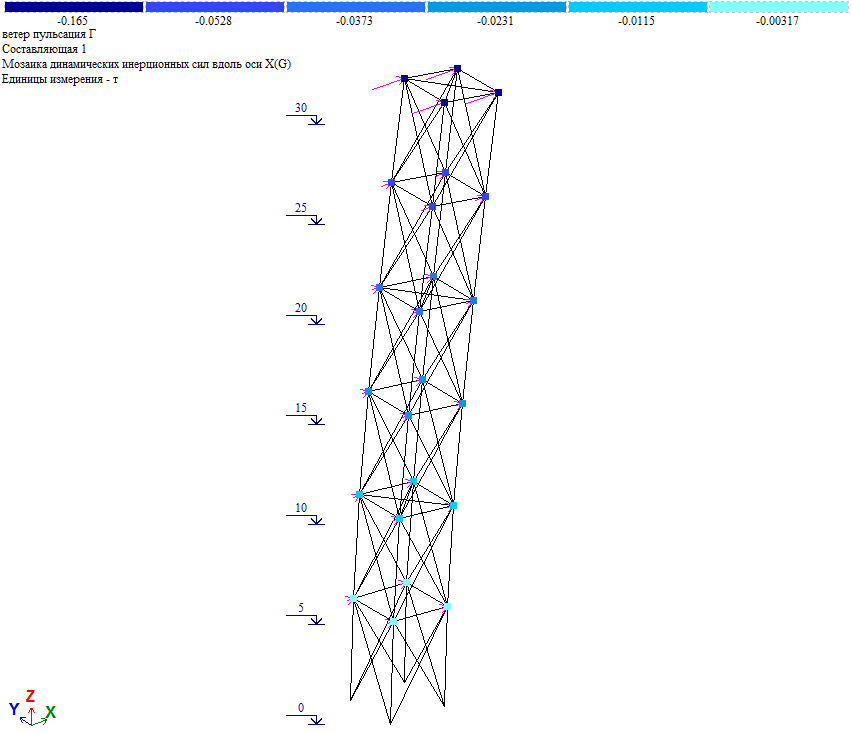
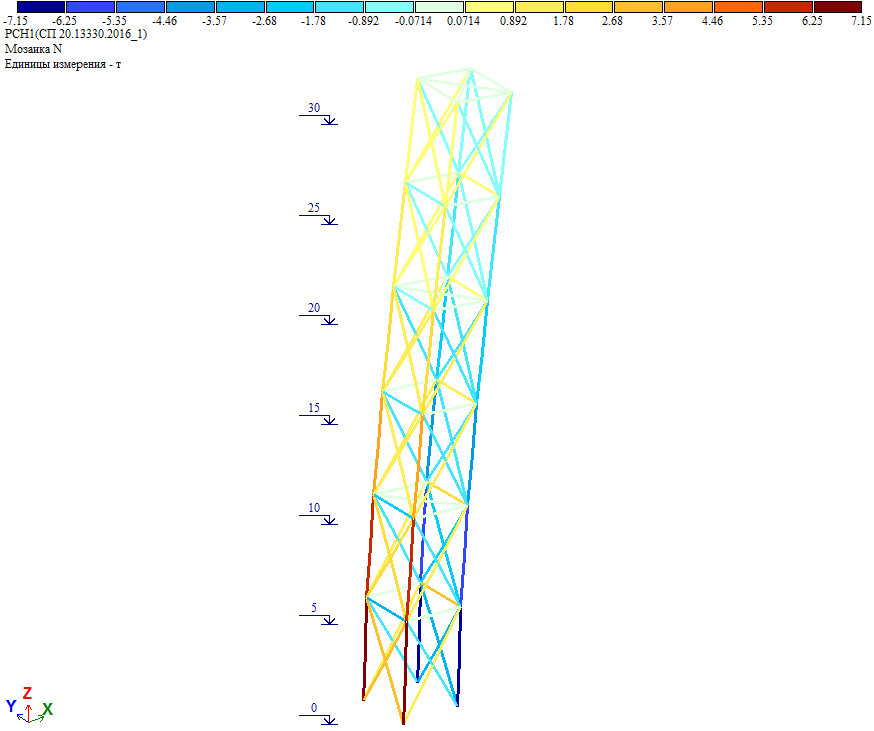
Как видно из результатов расчета, дополнительные массы не внесли значительный вклад в инерционные силы и внутренние усилия. Максимальное продольное усилие увеличилось на 100%*(7.15-7.13)/7.13=0.28%.
При действии ветра на диагональ следует ввести локальную систему координат узлов по направлению ветра. Для этого нужно отметить узлы, к которым прикладывается нагрузка, вызвать диалог «Локальные оси узлов» и указать в качестве координат точки, из которой будет смотреть ось X2, достаточно большие величины:
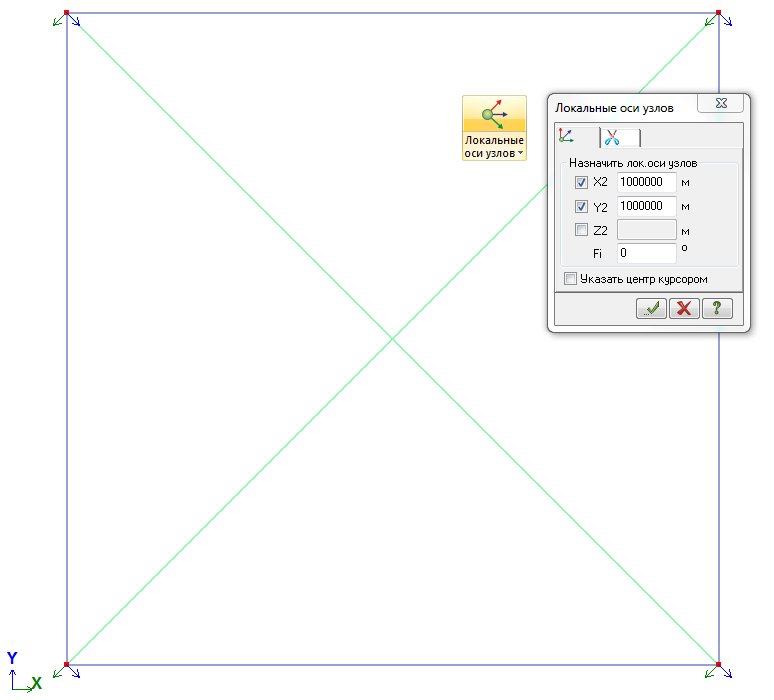
В итоге для узлов местные оси Х2 будут параллельны и сонаправлены с ветровым воздействием. Итоговая форма колебаний при определении величины ветровой пульсации также будет совпадать с направлением ветра на диагональ.
Инерционные силы:
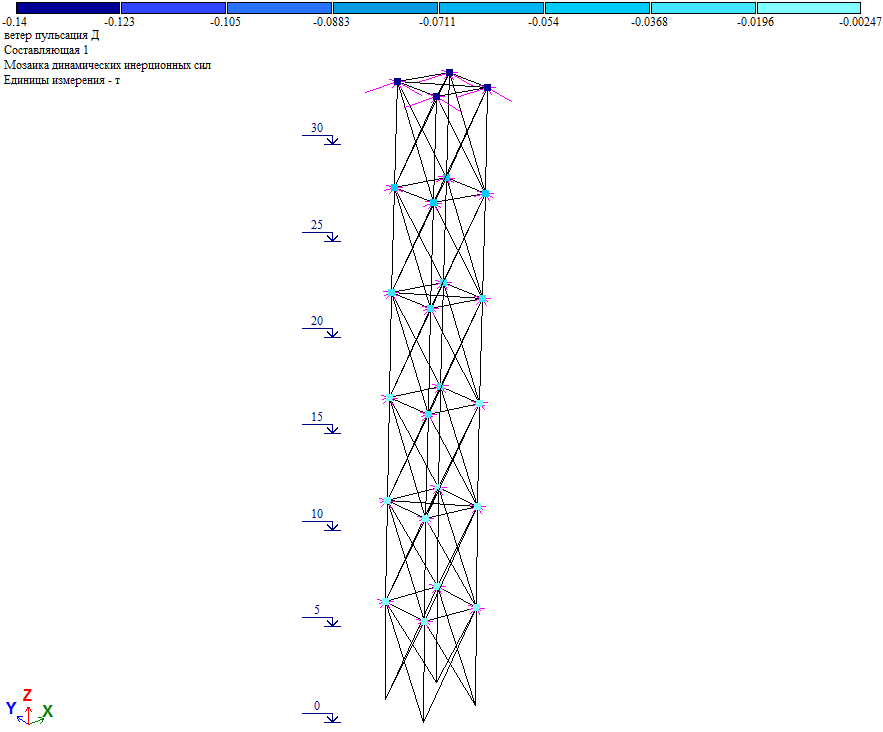
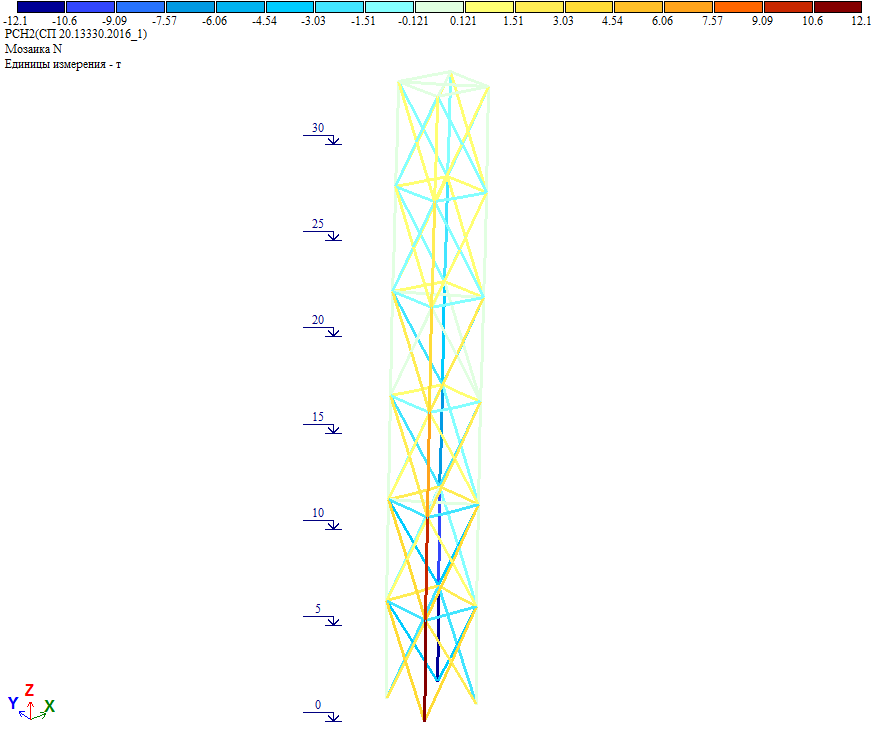
Как видно из результатов расчета, дополнительные массы не внесли значительный вклад в инерционные силы и внутренние усилия.
