Расчёт кирпичного простенка на косое внецентренное сжатие по нелинейной деформационной модели с подбором армирования
Исходные данные
Материал – кирпич керамический на ц.п. растворе. Марка кирпича М250, марка раствора М200. Расчётное сопротивление кладки сжатию R=36.7098 кгс/см2, Rt=0.815773 кгс/см2, Ru=2*R=2*36.7098=73.4196 кгс/см2, Rtu=2*Rt=2*0.815773=1.631546 кгс/см2. Размеры простенка b=100 см, h=51 см. Высота простенка l0=450 см. По результатам определения внутренних усилий в сечении простенка возникают следующие усилия: N=150 т, изгибающие моменты Мх=1.378 т*м, Му=1.075 т*м, поперечные силы, Qx=-0.378 т, Qy=0.502 т;
Определение деформационных характеристик кладки
Модуль деформации неармированной кладки при сжатии E=α*Ru=1000*73.4196=73419.6 кгс/см2.
Относительные деформации кладки при сжатии ε=R/E=36.7098/73419.6=0.0005
Относительные деформации для нелинейных расчётов
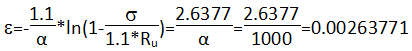
Определение предельных деформаций при сжатии
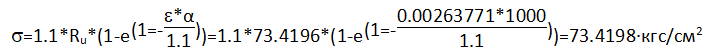
Модуль деформации неармированной кладки при растяжении Et=α*Rtu=1000*1.631546=1631.546 кгс/см2.
Относительные деформации кладки при растяжении εt=R/E=0.815773/1631.546=0.0005
Относительные деформации для нелинейных расчётов
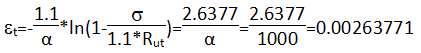
Определение предельных деформаций при растяжении
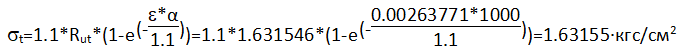
Расчёт на косое внецентренное сжатие
Определение площади сжатой части сечения Ас, расчётом в конструкторе сечений

По результатам расчёта получаем, что всё сечение сжато, следовательно: Ac=А=b*h=100*51=5100 см2
По п.7.7 Расчет внецентренно сжатых неармированных элементов каменных конструкций следует производить по формуле
N<=φ1*mg*R*Ac*ω
mg=1 — коэффициент, учитывающий влияние длительной нагрузки и определяемый по формуле (16). При толщине стены более 30 см, принимается равным 1.
φ1x=(φx+φcx)/2
φ — коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый по расчетной высоте элемента l0.
Расчёт в направлении стороны h. Для l0=290 см, ix=0.289*38=10.982 см, α=1000, по таблице 19, при λ=l0/ix=450/14.739=30.531, φ=0.90554
|
|
αn | |
| 1000 | ||
| λn | 28 | 0.92 |
| λi | 30.531 | 0.90554 |
| λn+1 | 35 | 0.88 |
φс — коэффициент продольного изгиба для сжатой части сечения, определяемый по фактической высоте элемента Н по таблице 18 в плоскости действия изгибающего момента при гибкости:
λiс=H/iс
где hс и iс — высота и радиус инерции сжатой части поперечного сечения Ас в плоскости действия изгибающего момента.
Высота сжатой части сечения hс=h=51 см;
Радиус инерции сжатой части сечения icx=0.289*hcx=0.289*51=14.739 см, λcx=l0/icx=450/14.739=30.531, φcx=0.90554
|
|
αn | |
| 1000 | ||
| λn | 28 | 0.92 |
| λi | 30.531 | 0.90554 |
| λn+1 | 35 | 0.88 |
Коэффициент продольного изгиба: φ1h=(φh+φch)/2=(0.90554+0.90554)/2=0.90554
e0x=Mx/N=0.919 см — эксцентриситет расчётной силы N относительно центра тяжести сечения в направлении стороны h;
Коэффициент ω=1+(ex+ev)/h=1+0.919/51=1.018 — для кладки из керамического кирпича
Подставляя данные в формулу прочности простенка, получаем:
N=16.057 т<=φ1h*mg*R*Ac*φh=0.90554*36.7098*1*5100*1.018=172.58681 т
Коэффициент запаса 172.58681/150=1.15058
Расчёт в направлении стороны b. Для l0=450 см, iy=0.289*100=28.9 см, α=1000, по таблице 19, при λ= l0/iy=450/28.9=15.57, φ=0.99103.
|
|
αn | |
| 1000 | ||
| λn | 14 | 1 |
| λi | 15.57 | 0.99103 |
| λn+1 | 21 | 0.96 |
φс — коэффициент продольного изгиба для сжатой части сечения, определяемый по фактической высоте элемента Н по таблице 18 в плоскости действия изгибающего момента при гибкости:
λiс=H/iс
где hс и iс — высота и радиус инерции сжатой части поперечного сечения Ас в плоскости действия изгибающего момента.
Высота сжатой части сечения bс=b=100 см;
Радиус инерции сжатой части сечения icb=0.289*bc=0.289*100=28.9 см, λcb=l0/icb=450/28.9=15.57, φcx=0.99103
|
|
αn | |
| 1000 | ||
| λn | 14 | 1 |
| λi | 15.57 | 0.99103 |
| λn+1 | 21 | 0.96 |
Коэффициент продольного изгиба: φ1b=(φb+φcb)/2=(0.99103+0.99103)/2=0.99103
e0b=My/N=0.779 см – эксцентриситет расчётной силы N относительно центра тяжести сечения в направлении стороны b;
Коэффициент ω=1+eb/h=1+0.779/100=1.008 — для кладки из керамического кирпича
Подставляя данные в формулу прочности простенка, получаем:
N=150 т<=φ1b*mg*R*Ac*φb=0.99103*36.7098*1*5100*1.008=187.02494 т
Характеристики материалов каменных конструкций, заданных для расчёта в программе
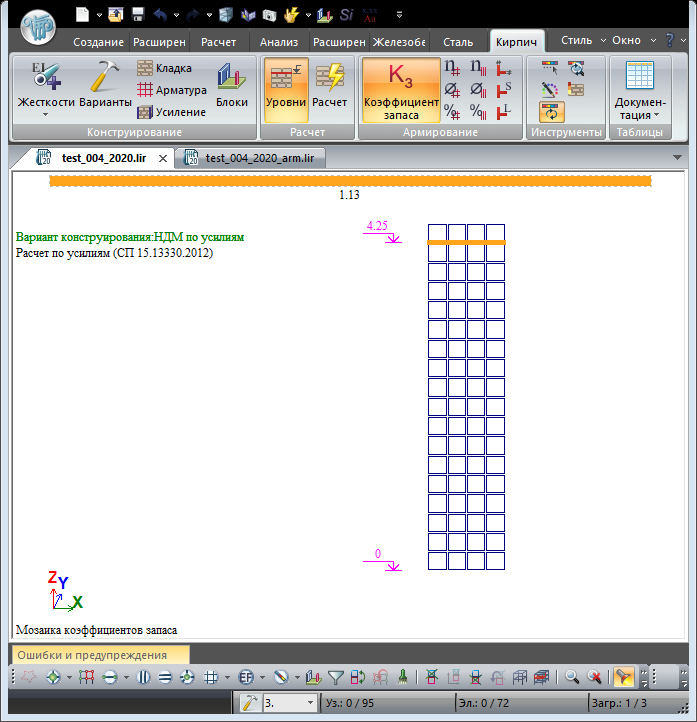
Расчёт в ПК ЛИРА САПР, выполняется по СП 15.13330.2012 по нелинейной деформационной модели кладки.
Характеристики материалов:

Сравнение результатов ручного расчёта с программным счётом
Сравнение выполним в табличной форме
| Параметр для сравнения | Результат расчёта | Погрешность | |
| Ручной расчёт | ЛИРА-САПР | ||
| Коэффициент запаса прочности кладки при сжатии (минимальное значение из результатов расчёта в двух направлениях) | 1.15058 | 1.13 | 1.79% |
Подбор армирования кирпичной кладки
Исходные данные
Выполним расчёт конструкции из предыдущего примера с уменьшенными марками кирпича и раствора. Марка кирпича М150, марка раствора М100. Расчётное сопротивление кладки сжатию R=22.432828 кгс/см2.
Несущая способность простенка при центральном сжатии:
Высота простенка и размеры поперечного сечения такие же, как при проверке неармированной кладки.
N=150 т>φ1h*mg*R*A=0.90554*1*22.432828*5100=103.600498 т — условие не выполняется, требуется сетчатое армирование.
Принимаем армирование сетками из арматуры В500, Rs=4435.77 кгс/см2, диаметр стержней 4 мм, шаг стержней 50x50 мм. Сетки устанавливаются через три ряда, при высоте ряда кладки 100 мм, шаг сеток будет равен 30 см. Определим расчётное сопротивление армированной кладки:
Rsk=R1+(p*μ*Rs)/100=22.432828(+2*0.16757*4435.77)/100=37.298868 кгс/см2
μ=(2*Ast)/(C*S)*100=2*0.1265*30*100=0.16757%
Проверка условия Rsk≤2*R
37.298868<2*22.432828 – условие выполняется, принимаем Rsk=37.298868 кгс/см2.
Определим упругую характеристику кладки с сетчатым армированием:
αsk=α*Ru/Rsku=α*(k*R)/(k*Rsk)=1000*(2*22.432828)/(2*37.298868)=601.43455291994
Расчёт несущей способности армированной кладки. Для l0=450 см, iy=0.289*51=14.739 см, по таблице 19, при λ=l0/iy=450/14.739=30.531, φ=0.84828691058.
|
|
αn | αi | αi+1 | |
| 750 | 601.43455291994 | 500 | ||
| λn | 28 | 0.9 | 0.87028691058 | 0.85 |
| λi | 30.531 | 0.878 | 0.84828691058 | 0.828 |
| λn+1 | 35 | 0.84 |
|
0.79 |
Подставляя данные в формулу прочности простенка, получаем:
N=100 т>φy*mg*Rsk*A=0.84828691058*1*37.298868*5100=161.36472166964 т
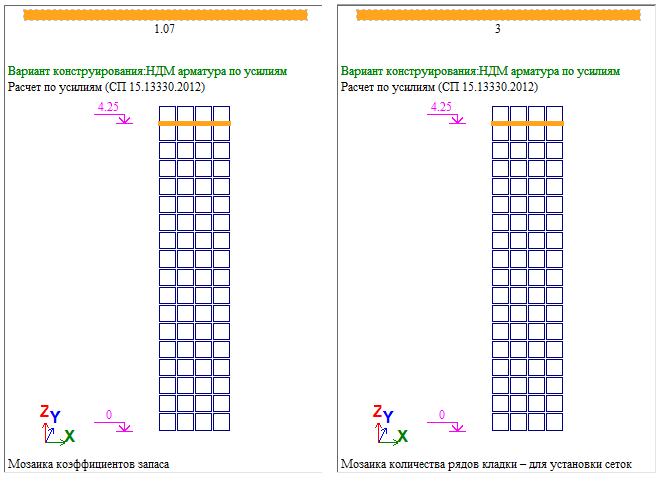
Условие прочности выполняется. Коэффициент запаса 161.36472166964/150=1.07576481113
Характеристики материалов каменных конструкций, заданных для расчёта в программе
Расчёт в ПК ЛИРА САПР, выполняется по СП 15.13330.2012 по нелинейной деформационной модели кладки.
Характеристики материалов:

Сравнение выполним в табличной форме
| Параметр для сравнения | Результат расчёта | Погрешность | |
| Ручной расчёт | ЛИРА-САПР | ||
| Коэффициент запаса прочности кладки при сжатии | 1.07576481113 | 1.07 | 0.54% |